Binäre Ganzzahldarstellung und binäre Operationen
Das binäre System (auch bekannt als Zahlensystem zur Basis 2) ist ein Zahlensystem, das nur zwei Zeichen verwendet, 0 und 1, um Zahlen darzustellen. erreicht einen numerischen Wert, diese Binärzahl system wird oft erwähnt, wenn man c, c++, einführende Programmierung und Informatik lernt. In diesem Artikel erfahren Sie, wie Sie eine Ganzzahl im Binärformat darstellen und Operationen im Binärformat ausführen.
Mục lục
1. Dezimaldarstellung in Binär:
Wir kommen zu einem Beispiel einer Zahl 31 und 33, wenn sie wie folgt binär dargestellt werden:
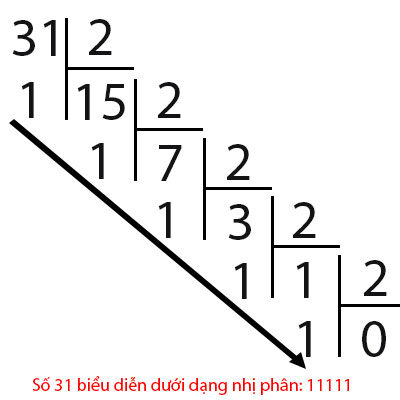
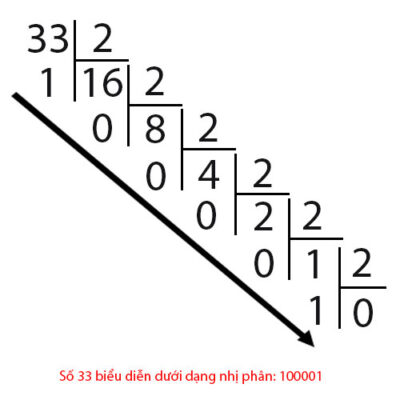
Wie stellt man also aus Binärzahlen Dezimalzahlen dar? Schauen wir uns das folgende Beispiel an:
2. Darstellen von Binärzahlen als Dezimalzahlen
Rechnen Sie für jede Einheit mit dem Wert 1 hoch 2 mal 1 mal von rechts und rechnen Sie nach folgender Formel:
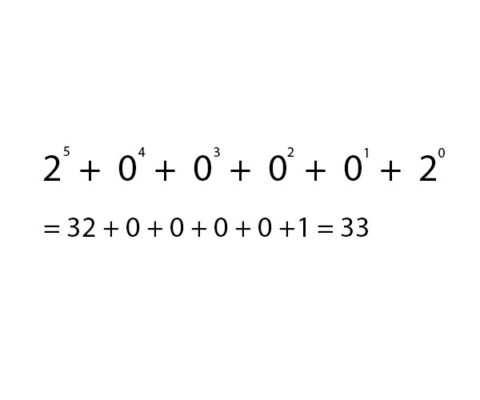
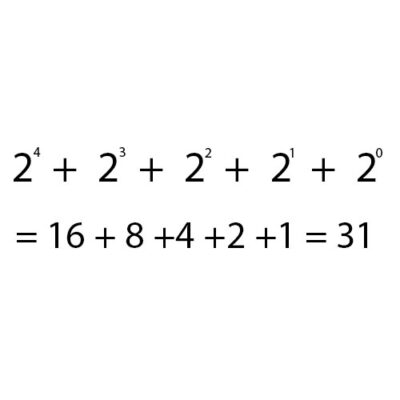
3. Addiere 2 Binärzahlen
Um zwei Binärzahlen zu addieren, wenden wir die Regel an:
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 (erinnere dich an 1)
Beispiel : Fügen Sie zwei Zahlen "1000111" und die Zahl "11110" hinzu
1 0 0 0 1 1 1 (71) + 1 1 1 1 0 (30) ------------- = 1 1 0 0 1 0 1 (101)4. Subtrahiere 2 Binärzahlen
Um 2 Binärzahlen zu subtrahieren, wenden wir die Regel an:
0 − 0 = 0 0 − 1 = 1 (geliehen 1) 1 − 0 = 1 1 − 1 = 0
1 1 0 1 1 1 0 − 1 0 1 1 1 --------------- = 1 0 1 0 1 1 1
5. Negative Zahlen binär darstellen
Bevor Sie das Konzept eingeben, können Sie diesen Link als Referenz lesen: https://en.wikipedia.org/wiki/Bi%E1%BB%83u_di%E1%BB%85n_s%E1%BB%91_%C3 %A2m As Wir haben verstanden, dass jedes Zeichen oder positive und negative Zahlen im Computer binär durch die Zahlen 0 und 1 dargestellt wird. Theoretisch gibt es viele Möglichkeiten, negative Zahlen im Computer darzustellen. Uns interessiert die Darstellung des Mengenzeichens und des Zweierkomplements Art der Darstellung des Mengenzeichens: Nach dem Prinzip der Mengenzeichendarstellung stellt das linke Bit das Vorzeichen dar, ein 8-Bit-Byte hat 7 Bits (minus das Bit).Zeichen) wird verwendet, um Zahlen von 0000000 (0 10 ) bis 1111111 (127 10 ) darzustellen. Bei Verwendung des Vorzeichenbits ändert sich die Bedeutung der oberen 7 Bits und wir können Zahlen von −127 10 bis +127 10 darstellen. Bei der Vorzeichenmethode kann die Zahl 0 in zwei Formen dargestellt werden, nämlich 00000000 (+0) und 10000000 (−0).
Diese Methode kann jedoch leicht Verwirrung stiften, zum Beispiel: Die Zahl 143 wird in eine Binärzahl umgewandelt, die Zahl wird als 10001111 dargestellt, aber versuchen Sie dieses Programm auf c: #include <stdio.h> #include <stdlib.h> void writebitwise(int n){ char buffer [33]; itoa (n,buffer,2); printf ("binary: %sn",buffer); } int main(){ int n = 10; writebitwise(-15); } Die Zahl -15 wird als Folge 1111111111111111111111111110001 (10001111) dargestellt, was leicht zu verwechseln ist und bei Berechnungen mit Binärzahlen wegen des Vorzeichens ziemlich verwirrend ist. Wir gehen zur 2er-Komplement-Methode zur Darstellung negativer Binärzahlen über:
- Erstens ist das Vorzeichenbit 0, wenn die Zahl positiv ist, und 1, wenn die Zahl negativ ist.
- Verwenden Sie zweitens den bitweisen Operator NOT, um alle Bits einer positiven Binärzahl zu invertieren (berechnen Sie das Vorzeichenbit), um die entsprechende negative Zahl darzustellen.
Beispiel: Die binär dargestellte Zahl 5 10 wäre 00000101. Die binär dargestellte Zahl −5 10 (8-Bit-Nenner) ist 11111010. Um das Zweierkomplement darzustellen, addieren Sie 1 zur Zahl. binär im 1er-Komplement, was 1 hinzufügt 11111010: 11111010 + 1 = 11111011. 11111011 ist also die Zweierkomplementdarstellung von −5 10 in einem Computer.
Bài viết liên quan:
Dịch vụ thiết kế Wesbite
