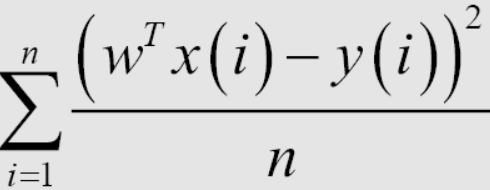
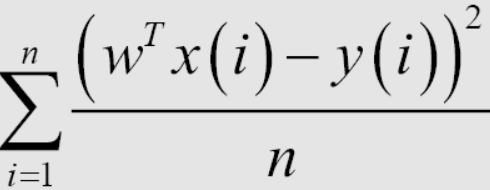
Lineares Regressionsmodell
- 24-07-2022
- chuong xuan
- 0 Comments
Wir verwenden zwar die verfügbaren Bibliotheken, um das Modell zu trainieren, aber wir verwenden einen Verriegelungslöffel, um eine Schachtel zu öffnen, ohne zu wissen, was sich darin befindet? Aber Sie können die Box immer noch öffnen. Mit einem besseren Verständnis der Theorien innerhalb des Algorithmus können Sie die Parameter verwenden, um das Modell anzupassen.
In diesem Abschnitt mache ich Sie mit der linearen Regression vertraut, die einer der grundlegendsten Algorithmen des maschinellen Lernens ist. Bei diesem Algorithmus werden Input und Output durch eine lineare Funktion beschrieben.
Mục lục
Illustrierte mathematische Aufgabe
Angenommen, es gibt ein Problem bei der Vorhersage von Hauspreisen. Es gibt Daten von 1000 Häusern in dieser Stadt, in denen wir die Parameter im Wort Haus kennen, ist die Breite ist x 1 m 2 hat x 2 Schlafzimmer und ist 3 km vom Zentrum entfernt. Wenn Sie ein neues Haus mit den obigen Parametern hinzufügen, können Sie den Preis y des Hauses vorhersagen? Wenn ja, wie sieht die Prädiktorfunktion y = f(x) aus? Hier ist der Merkmalsvektor x = [x 1, x 2 , x 3 ] T ein Spaltenvektor, der Eingabeinformationen enthält, die Ausgabe y ist ein Skalar.
Tatsächlich können wir sehen, dass mit zunehmenden Koeffizienten der Wortmerkmale auch die Ausgabe zunimmt, sodass es eine einfache lineare Funktion gibt:
y_pre = f(x) = w 0 + w 1 x 1 + w 2 x 2 + … + w n x n = x T w
Da drin:
- y_pre: ist der vorhergesagte Ausgangswert. (und y_pre unterscheidet sich vom tatsächlichen y)
- n ist die Anzahl der Merkmale.
- (x i ) ist das i .te Merkmal
- w ist der Parameter des Modells, wobei w 0 die Abweichung ist und die Parameter w 1 , w 2 , ….
Das obige Problem ist das Problem der Vorhersage des Werts der Ausgabe basierend auf dem Eingabemerkmalsvektor. Außerdem kann der Wert der Ausgabe viele verschiedene positive reale Werte annehmen. Es handelt sich also um ein Regressionsproblem. Die Beziehung y_pre = x T w ist eine lineare Beziehung. Von hier kommt der Name lineare Regression.
Modelltraining
Nach einem linearen Regressionsmodell geht es beim Training des Modells darum, die optimalsten Parameter durch den Trainingsdatensatz zu finden. Dazu brauchen wir einen Weg, um festzustellen, ob das Modell gut ist oder nicht. Hier stelle ich eine Methode zur Bestimmung vor, die darin besteht, den Ausdruck Root Mean Square Error (RMSE) zu verwenden. Das Ziel dieses Trainings ist es, den Wert des mittleren quadratischen Fehlers (MSE) zu minimieren. Es bedeutet einfach, dass der Unterschied zwischen dem vorhergesagten y und dem tatsächlichen y so gering wie möglich sein soll.
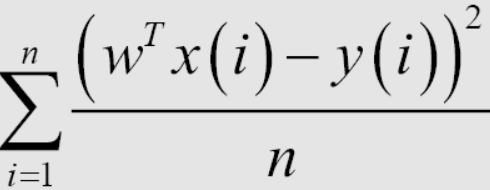
Durchschnitt 1/n oder Summe in der Verlustfunktion hat mathematisch keinen Einfluss auf die Lösung des Problems. Beim maschinellen Lernen enthalten die Verlustfunktionen normalerweise den durchschnittlichen Koeffizienten für jeden Datenpunkt im Trainingssatz. Wenn wir also den Wert der Verlustfunktion im Testsatz berechnen, müssen wir den durchschnittlichen Fehler jedes Punkts berechnen. Die Berechnung der Verlustfunktion hilft, eine Überanpassung zu vermeiden, wenn die Anzahl der Datenpunkte zu groß ist, und hilft uns auch, das Modell später zu evaluieren.
Standardgleichung
Um den Wert von w zu finden, der der obigen Gleichung hilft, ihren Minimalwert zu erreichen, können wir die Ableitung der oberen Richtung in Bezug auf w berechnen, wenn sie Null sind. Und bestimme das Minimum.
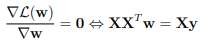
Daher können wir das Minimum durch die folgende Formel bestimmen: w = (X T X) – 1XTy.
Wobei w der Wert ist, bei dem MSE(w) minimiert wird. y ist der zu findende Vektor einschließlich (y 1 , … y m ).
In Python implementieren.
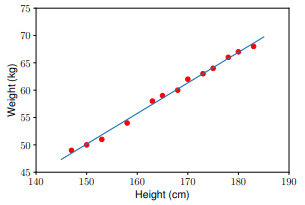
Bestimmen Sie unter Annahme des unten stehenden Datensatzes das Gewicht dieser Person anhand der Körpergröße.
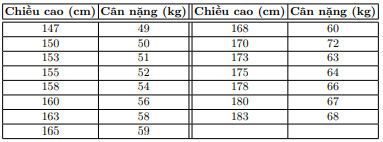
Datenanzeige
import numpy as np
import matplotlib.pyplot as plt
X = np.array([[147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183]]).T
y = np.array([ 49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68])
Wenn wir uns das Problem ansehen, müssen wir das Modell der Form bestimmen: (Gewicht) = w_1*(Höhe) + w_0.
Bestimmen Sie die Lösung nach der Formel.
Daten initialisieren
one = np.ones((X.shape[0], 1)) #Bias
Xbar = np.concatenate((one, X), axis = 1) # each point is one row
Als nächstes berechnen wir die Koeffizienten w_1 und w_0 nach der Formel . Hinweis: Die Pseudo-Inverse einer Matrix A in Python wird mit numpy.linalg.pinv(A ) berechnet.
A = np.dot(Xbar.T, Xbar)
b = np.dot(Xbar.T, y)
w_best = np.dot(np.linalg.pinv(A), b)
Verwenden Sie das Modell, um die Daten in der Testreihe vorherzusagen:
y1 = w_1 * 155 + w_0
y2 = w_1 * 160 + w_0
print('Input 155cm, true output 52kg, predicted output %.2fkg' %(y1) )
print('Input 160cm, true output 56kg, predicted output %.2fkg' %(y2))
Ergebnis
Input 155cm, true output 52kg, predicted output 52.94kg
Input 160cm, true output 56kg, predicted output 55.74kg
Sie können auch mit einigen Python-Bibliotheken versuchen, die Ergebnisse zu vergleichen.
Probleme, die durch lineare Regression gelöst werden können
Wir sehen, dass die Formel X T W eine lineare Funktion sowohl von w als auch von x ist. Aber tatsächlich kann die lineare Regression auf Modelle angewendet werden, die nur bezüglich w linear sein müssen. Zum Beispiel:
y w 1 x 1 + w 2 x 2 + w 3 x 2 1 + w 4 sin(x 2 ) + w 5 x 1 x 2 + w 0
Ist eine lineare Funktion von w und kann daher auch durch lineare Regression gelöst werden. Die Bestimmung von sin(x2) und x1x2 ist jedoch relativ unnatürlich.
Einschränkungen der linearen Regression
Die erste Einschränkung der linearen Regression besteht darin, dass sie sehr rauschempfindlich ist. Wenn im obigen Beispiel für die Beziehung zwischen Größe und Gewicht nur ein verrauschtes Datenpaar (150 cm, 90 kg) vorhanden ist, werden die Ergebnisse sehr unterschiedlich sein.
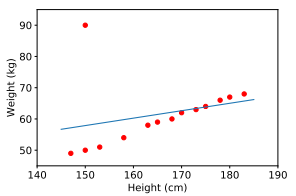
Vor der Implementierung des Trainingsmodells benötigen wir also einen Schritt namens Vorverarbeitung, über den ich im vorherigen Blog gesprochen habe, auf den Sie sich beziehen können.
Die zweite Einschränkung der linearen Regression besteht darin, dass sie keine komplexen Modelle darstellen kann.
Zusammenfassung
In diesem Artikel habe ich Ihnen gezeigt, wie Sie einen linearen Regressionsalgorithmus trainieren. Grundsätzlich braucht man zum Trainieren eines Algorithmus:
- Definieren Sie das Modell.
- Definieren Sie eine Kostenfunktion (oder Verlustfunktion).
- Optimierung der Kostenfunktion anhand von Trainingsdaten.
- Finden Sie die Modellgewichte, bei denen die Kostenfunktion den kleinsten Wert hat.