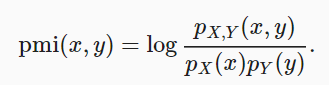
Merkmalsauswahlmethode beim maschinellen Lernen.
- 24-07-2022
- chuong xuan
- 0 Comments
Tatsächlich sind nicht alle Daten klar, die Funktionen sind für das Modell nützlich. Wenn wir zum Beispiel den Preis eines Hauses vorhersagen wollen, spielt es keine Rolle, ob der Vermieter ein Junge oder ein Mädchen ist. Daher ist es sehr wichtig, Funktionen auszuwählen, die für das Modell nützlich sind, um die Anzahl der Eingabedatendimensionen zu reduzieren.
Grundsätzlich verwenden wir die Wahrscheinlichkeit, um die Beziehung zwischen jedem Merkmal und dem vorherzusagenden Zielfeld zu berechnen. Aber die Idee ist, dass es immer noch eine große Weisheit ist, eine Formel oder ein Maß zu verwenden, um festzustellen, dass die Funktion nicht gut ist. In diesem Artikel werden Sie und ich durch einige Formeln und Berechnungen lernen!
Mục lục
Merkmalsauswahlmethode
Merkmalsauswahlalgorithmen können in drei Kategorien unterteilt werden: Filterverfahren, Wrapperverfahren und eingebettete Verfahren.
Filter
Dieser Typ hat folgende Eigenschaften:
- Hängt von den Eigenschaften der Daten ab
- Bietet eine geringere Leistung als Wrapper-Methoden oder eingebettete Methoden.
- Methoden: Varianz , Korrelation , Univariate Auswahl , Multivariate Auswahl .
Informationen zu konstanten, quasi-konstanten, duplizierten Merkmalen.
Konstante Merkmale : Zeigt nur einen Wert für alle Beobachtungen im Datensatz an.
Die einfachste Methode zum Umgang mit konstanten Features. Wir werden einen Schwellenwert (Schwellenwert) für die Varianz festlegen, Merkmale, die diesen Schwellenwert nicht erreichen, werden verworfen. (Kann sklearn zur Verarbeitung verwenden)
aus sklearn.feature_selection import VarianceThreshold sel = VarianceThreshold(Schwellenwert=0) # fit findet die Features mit Null-Varianz. sel.fit(X_train) # Die Methode get_support() gibt zurück, welche Features beibehalten werden. Retained_features = sel.get_support()
Es wird eine boolsche Sequenz zurückgegeben, wir müssen sie uns nur ansehen, um zu wissen, welche Features die Bedingung nicht erfüllen.
Quasi-konstante Merkmale : Ähnlich wie bei den oben genannten konstanten Merkmalen können wir nur den Schwellenwert anpassen, um die Bedingung strenger zu machen (z. B. Schwellenwert = 0,01, das Merkmal wird gelöscht, wenn es einen Wert von 99 % hat. gleichermaßen).
Duplizierte Features : Sind ähnliche Features, z. B. ein Original-Feature und ein anderes Feature ist der Label-Encoder des Original-Features, dann sind diese beiden Features gleichwertig, wir können ein Feature weglassen. Oder mehrere identische Zeilen.
Methode:
- Für kleine Datensätze: In Pandas gibt es eine Funktion zum Auswerten, ob ein Datenrahmen doppelte Zeilen enthält. Um die Spalten zu überprüfen, verwenden wir immer noch die Duplicated()-Funktion, transponieren einfach die Matrix.
- Mit großem Datensatz: Wenn die Verwendung von Transpose mit großen Daten definitiv sehr speicherintensiv und nicht machbar ist. So können wir loop verwenden, um doppelte Spalten zu finden, oder die numpy-Bibliothek verwenden.
for_, idx = np.unique(df.to_numpy(), axis=1, return_index=True) df_uniq = df.iloc[:, np.sort(idx)]
Korrelation
Die Verwendung der Korrelation zwischen zwei oder mehr Variablen ist auch eine gute Möglichkeit, Features mit geringer Korrelation zu entfernen. Das Entfernen stark korrelierter Merkmale trägt dazu bei, dass das lineare Modell besser funktioniert, wodurch Verzerrungen zwischen Merkmalen vermieden werden.
- Wir können die Funktion mit einem niedrigen Korrelationsziel testen, wir können die Funktion löschen.
- Oder überprüfen Sie die Korrelation zwischen Merkmal und Merkmal, wenn zwei Merkmale eine hohe Korrelation miteinander aufweisen. Möglicherweise haben diese beiden Merkmale dieselben Informationen, und wir können 1 Merkmal auslassen, um die Dimensionalität der Eingabedaten zu verringern.
So bestimmen Sie den Korrelationskoeffizienten .
Korrelationskoeffizient nach Pearson
Summe((x1 - x1.Mittelwert) * (x2 - x2.Mittelwert) * (xn - xn.Mittelwert)) / var(x1) * var(x2) * var(xn)
- Der Pearson-Koeffizient hat einen Wert im Bereich [-1,1]
- Die Idee ist, die Korrelation zwischen Merkmalen zu berechnen. Wenn 2 Merkmale eine Korrelation aufweisen, die größer ist als der von mir festgelegte Schwellenwert, lasse ich eines dieser 2 Merkmale fallen.
corrmat = X_train.korr()
# Handlung
fig, ax = plt.subplots()
fig.set_size_inches(11,11)
sns.heatmap(korrmat)
def Korrelation (df, Schwelle):
col_corr = set()
corrmat = df.korr()
für i in range(len(corrmat.columns)):
für j im Bereich (i):
# Interesse an ABS-Koeffizientenwerten
if abs(corrmat.iloc[i, j]) > Schwelle:
col_corr.add(corrmat.columns[i])
col_corr zurückgeben
corr_feats = Korrelation (X_train, 0,8)
X_train.drop(labels=corr_feats, axis=1, inplace=True)Statistische Maßnahmen
Es gibt einige Methoden und Kriterien für die Auswahl von Merkmalen nach statistischen Methoden:
- Informationsgewinn
- Univariate ROC-AUC/RMSE
Für jede der oben genannten Methoden gibt es 2 Schritte wie folgt:
- Bewerten Sie Merkmale nach einem bestimmten Kriterium: Jedes Merkmal wird unabhängig von anderen Merkmalen bewertet, wenn seine Beziehung zum Ziel betrachtet wird.
- Auswahl hochrangiger Merkmale: Können wir Klassifizierungs- oder Regressionsmodelle anwenden, um ein hochrangiges Merkmal zu bewerten?. Und wie viel Sie wissen müssen, ob das Ranking hoch oder niedrig ist, hängt natürlich von Ihnen ab.
Ein paar Vorbehalte: Wir können duplizierte oder verwandte Funktionen anwenden, bevor wir diesen Schritt ausführen. Und diese Methode hat auch einen großen Nachteil, dass 2 Features miteinander kombiniert werden können, es wirkt sich auf das Ziel aus und wenn wir diese Methode nur auf jedes Feature in Bezug auf Tagert anwenden, kann es zu Fehlern führen. Daher ist es notwendig, mehr Methoden anzuwenden, um zwischen Merkmalen und Zielen zu evaluieren.
Gegenseitige Information (Informationsgewinn)
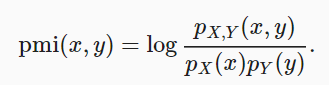
Diese Methode vergleicht die Wahrscheinlichkeit, dass x und y gleichzeitig über die Verteilung hinweg auftreten, und kombiniert sie mit dem Fall, dass die beiden Verteilungen unabhängig sind.
gegenseitige Information = sum{i,y} P(xi, yj) * log(P(xi,yj)/P(xi)*P(yj))Wenn x und y unabhängig sind, ist die gegenseitige Information 0.
Wir können die Python-Bibliothek verwenden, um Funktionen auszuwählen:
- Verwenden Sie
sklearn.feature_selection.mutual_info_regressionfür das Regressionsmodell. - Und
mutual_info_classifzur Auswahl mit Modellklassifikation.
Führen Sie eine gegenseitige Informationsberechnung zwischen Variablen und Zielen durch. Gibt gegenseitige Informationen für jedes Feature zurück. Je kleiner der Wert, desto weniger Informationen über diese Funktion mit dem Ziel. (Vor der Anwendung dieser Methode wird eine Vorverarbeitung empfohlen).
Univariate ROC-AUC/RMSE
Die Idee ist, den ROC-AUC jedes Merkmals zu berechnen und dann das maschinelle Lernmodell zu verwenden, um das Ziel vorherzusagen. Hier können wir den Entscheidungsbaum verwenden und nach ROC-AUC oder RMSE auswerten. Von dort aus werden wir Merkmale mit hohen Metriken auswählen.
# bnp-paribas-Datensatz verwenden roc_vals = [] für feat in X_train.columns: clf = DecisionTreeClassifier() clf.fit(X_train[feat].fillna(0).to_frame(), y_train) y_scored = clf.predict_proba(X_test[feat].fillna(0).to_frame()) roc_vals.append(roc_auc_score(y_test, y_scored[:,1]))
rocvals = pd.Series(roc_vals) rocvals.index = X_train.columns rocvals.sort_values(ascending=False) # Anzahl von Features zeigt einen Roc-auc-Wert, der höher als zufällig ist. len(rocvals[rocvals>0.5])
Zusammenfassung:
Durch diese Studie haben Sie und ich einige Methoden der Merkmalsauswahl kennengelernt, wodurch die Anzahl der Eingabedimensionen reduziert wurde, um das Training des Modells zu vereinfachen.