Ausreißer oder Ausreißer sind Datenpunkte, die sich von der Datumsübersicht unterscheiden. Angenommen, der Alterswert ist negativ oder ein Land ist nicht auf der Karte aufgeführt. Wir können einige Funktionen in Python vollständig verwenden, um die Ausreißer zu bestimmen.

Beispiel für Ausreißer : Angenommen, eine Klasse hat 100 Schüler, von denen 99 4 Punkte und der andere 10 Punkte erhält. In einer anderen Klasse bekam jeder in der Klasse 6 Punkte. Wenn Sie also beurteilen möchten, welche Klasse besser ist, müssen Sie den Durchschnitt jedes Schülers in jeder Klasse bestimmen. Wenn die Gesamtpunktzahl berechnet wird, hat Klasse A natürlich eine höhere Punktzahl, aber in Wirklichkeit ist Klasse B besser.

Aliens im maschinellen Lernen

Wenn die Daten Ausreißer aufweisen, wirkt sich dies definitiv auf die Qualität des Modells aus. Schauen Sie sich das folgende Beispiel an:

Es gibt einen Standarddatensatz, der die Größe und das Gewicht jeder Person enthält, und einen Datensatz, der einige Ausreißer enthält.

pandas als pd importieren
df_example = pd.DataFrame(
    Daten={
        "Höhe": [147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "Gewicht": [49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
        "Höhe_2": [110, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "Gewicht_2": [49, 90, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
  } ) df_example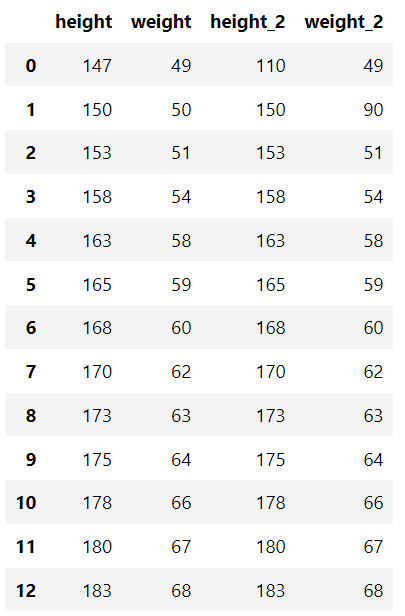

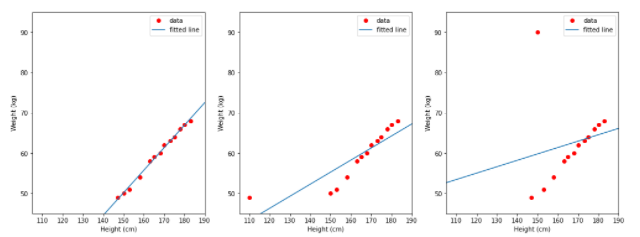
Wenn man sich die obigen Daten ansieht, sieht man, dass Größe und Gewicht direkt proportional sind, was bedeutet, dass ein Mann umso schwerer wird, je größer er ist. Vielleicht passt das lineare Regressionsmodell zu diesen Daten. Betrachten wir 3 Fälle, um die Ergebnisse des linearen Modells zu bestimmen.

• TH1 (links): Verwenden Sie die Daten in der Höhenspalte als Eingabe, in der Gewichtsspalte als Beschriftung.
• TH2 (Mitte): verwendet die Daten in der Spalte height_2 als Eingabe, in der Spalte weight als Label.
• TH3 (rechts): Verwenden Sie die Daten in der Spalte „height“ als Eingabe, in der Spalte „weight_2“ als Label.

 from matplotlib import pyplot as plt from sklearn.linear_model import LinearRegression
def fit_linear_regression_and_visualize( df: pd.DataFrame, input_col: str, label_col: str ): # fit the model by Linear Regression lin_reg = LinearRegression(fit_intercept= True ) lin_reg.fit(df[[input_col]], df[label_col]) w1 = lin_reg.coef_ w0 = lin_reg.intercept_ # visualize plt.plot(df[input_col], df[label_col], "ro", label="data") plt.axis([105, 190, 45, 75]) plt.xlabel("Height (cm)") plt.ylabel("Weight (kg)") plt.ylim(45, 95) plt.plot([105, 190], [w1 * 105 + w0, w1 * 190 + w0], label="fitted line") plt.legend() plt.figure(figsize=(17, 6)) plt.subplot(1, 3, 1) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight") plt.subplot(1, 3, 2) fit_linear_regression_and_visualize(df_example, input_col="height_2", label_col="weight") plt.subplot(1, 3, 3) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight_2")

Die blaue Linie ist die Linie, die das Modell gelernt hat. Wenn wir uns die 3 obigen Bilder ansehen, können wir sehen, dass die Zahl links von der Linie ziemlich konsistent mit den Daten ist. Daher gibt es einen einfachen Kommentar, ob Ausreißerdaten in der Eingabe des Modells oder in der Ausgabebezeichnung die Korrektheit des Modells beeinflussen.

Wie man Ausreißer identifiziert und handhabt, die Zahlen sind.

Es gibt 2 Haupttypen von Ausreißern:

• Die Werte liegen nicht im angegebenen Bereich der Daten. Beispielsweise dürfen Alter, Punktzahl oder Distanz nicht negativ sein.
• Der Wert wird wahrscheinlich eintreten, aber die Wahrscheinlichkeit ist sehr gering. Beispiel: Ein Schüler, der den Test 100 Mal macht, erhält 1 Punkt, aber 1 Mal erhält er 10 Punkte. Diese Werte kommen wahrscheinlich vor, sind aber wirklich selten.

Handhabung :

• Bei Daten in der ersten Gruppe können wir sie durch nan ersetzen und diesen Wert als fehlend betrachten und mit der Verarbeitung im fehlenden Datenverarbeitungsschritt fortfahren.
• Für Daten in der zweiten Gruppe wird normalerweise die Ober- oder Untergrenzenmethode (Clipping oder Capping) verwendet. Das heißt, ist ein Wert zu groß oder zu klein, bringen wir ihn auf den Maximal- oder Minimalwert, der als Punkt gilt, der nicht im Ausreißer liegt. Wenn es zum Beispiel eine Stadt in Längen- und Breitengrad außerhalb der Grenzen der Karte gibt, können wir sie in Bezug auf Breiten- und Längengrad betrachten, die ihr am nächsten sind, und keine Ausnahme. (Sie können Python verwenden, um den Ausnahmebereich zu bestimmen.)

IQR-Methode.

Um die Verwendung des Boxplots zu veranschaulichen, verwenden wir den Datensatz California Housing.

import pandas as pd housing_path ="https://media.githubusercontent.com/media/tiepvupsu/tabml_data/master/california_housing/" df_housing = pd.read_csv(housing_path + "housing.csv") df_housing.head()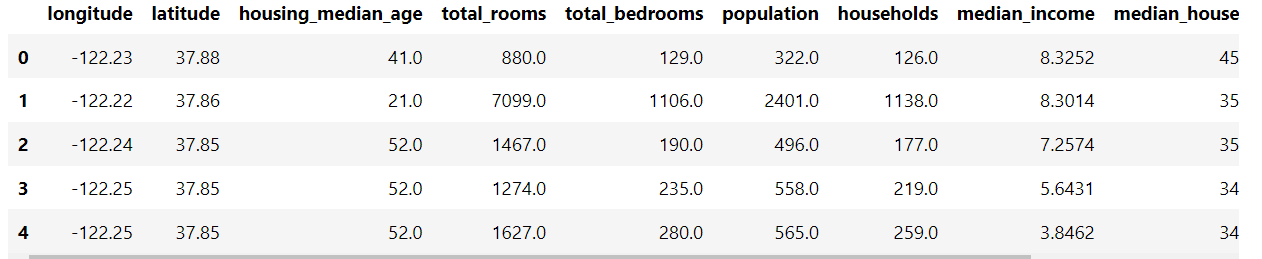

Unten sehen Sie das Histogramm und den Boxplot der Spalte total_rooms

import matplotlib.pyplot as plt fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5)) df_housing[["total_rooms"]].hist(bins=50, ax=axes[0]); df_housing[["total_rooms"]].boxplot(ax=axes[1], vert= False );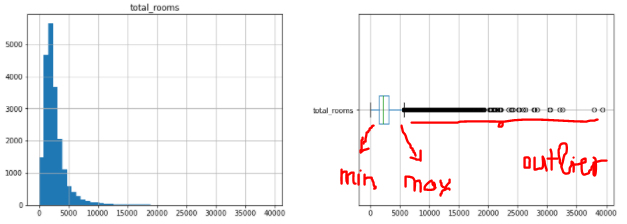

Wir sehen in der Abbildung, dass es ziemlich viele sporadische Werte nach rechts gibt. Also müssen wir sie auf den minimalen oder maximalen Wert von Boxplot bringen. Hier verwende ich die sklearn-API, um dies zu tun.

from typing import Tuple from sklearn.base import BaseEstimator, TransformerMixin def find_boxplot_boundaries( col: pd.Series, whisker_coeff: float = 1.5 ) -> Tuple[float, float]: """Findx minimum and maximum in boxplot. Args: col: a pandas serires of input. whisker_coeff: whisker coefficient in box plot """ Q1 = col.quantile(0.25) Q3 = col.quantile(0.75) IQR = Q3 - Q1 lower = Q1 - whisker_coeff * IQR upper = Q3 + whisker_coeff * IQR return lower, upper class BoxplotOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, whisker_coeff: float = 1.5): self.whisker = whisker_coeff self.lower = None self.upper = None def fit(self, X: pd.Series): self.lower, self.upper = find_boxplot_boundaries(X, self.whisker) return self def transform(self, X): return X.clip(self.lower, self.upper)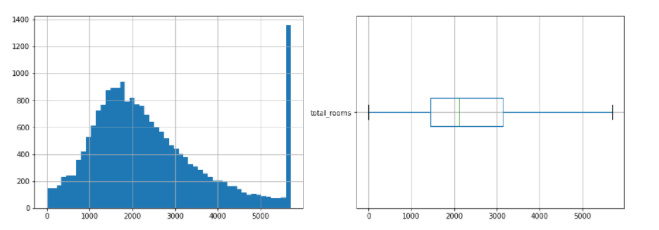

Eine kleine Erklärung, was IQR-Inter Quartile Range unter Verwendung des mittleren Quartilbereichs bedeutet, bestimmt dadurch, welche Werte außerhalb des Bereichs -1,5xIQR bis 1,5xIQR als Ausreißer gelten.

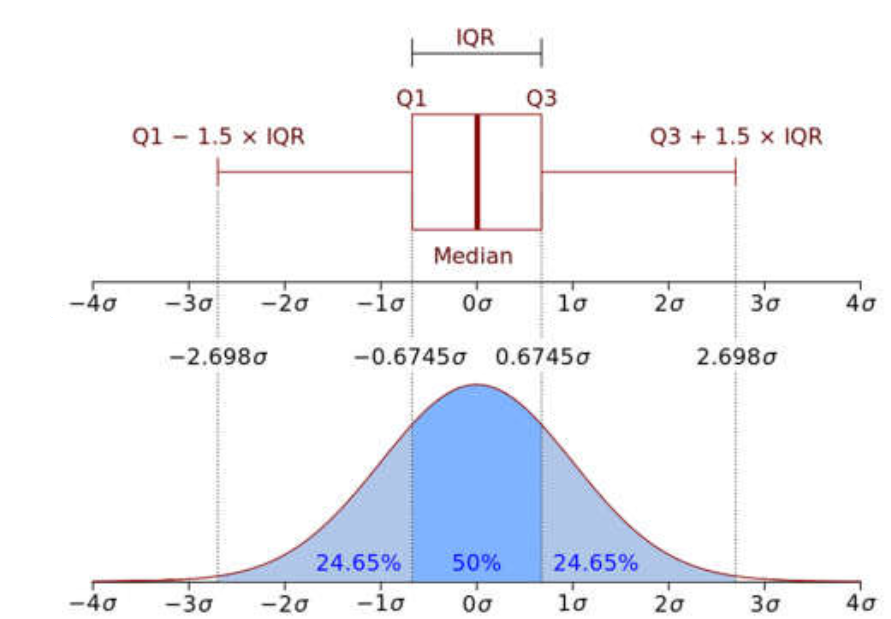
• (Q1–1,5 IQR) stellt den Mindestwert des Datensatzes dar.
• (Q3+1,5 IQR) Repräsentiert den Maximalwert des Datensatzes.

Nachdem wir die Daten gemäß dem Maximum und Minimum des Boxplots aufgeteilt haben, sehen wir, dass die Daten weniger verzerrt sind. Und wir sehen keine Ausreißer mehr außerhalb des Maximums und Minimums.

Die Z-Score-Methode .

Wenn die Daten einer Normalverteilung folgen, können Sie die 3σ-Regel auf die Normalverteilung anwenden.

Bei einer Normalverteilung sei μ der Erwartungswert und σ die Standardabweichung. Die 3σ-Regel für die Normalverteilung besagt:

• 68 % der Datenpunkte liegen innerhalb von μ±σ
• 95 % der Datenpunkte liegen innerhalb von μ±2σ
• 99,7 % der Datenpunkte liegen innerhalb von μ±3σ

Für einen Datenpunkt wird sein Z-Score wie folgt berechnet:

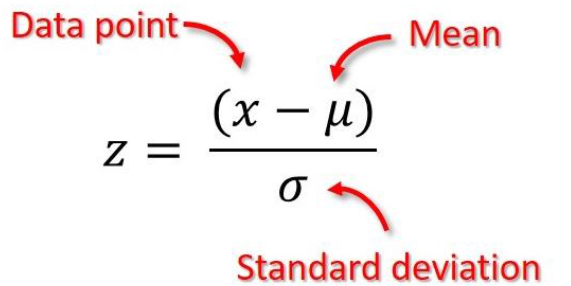
Daher liegen Punkte mit z-Wert, die als Ausreißer betrachtet werden können, außerhalb des Bereichs [-3, 3]. Wenn Sie die Mathematik ein wenig ändern, entspricht dies der Behandlung von Punkten außerhalb des Intervalls [μ−3σ,μ+3σ] als Ausreißer.

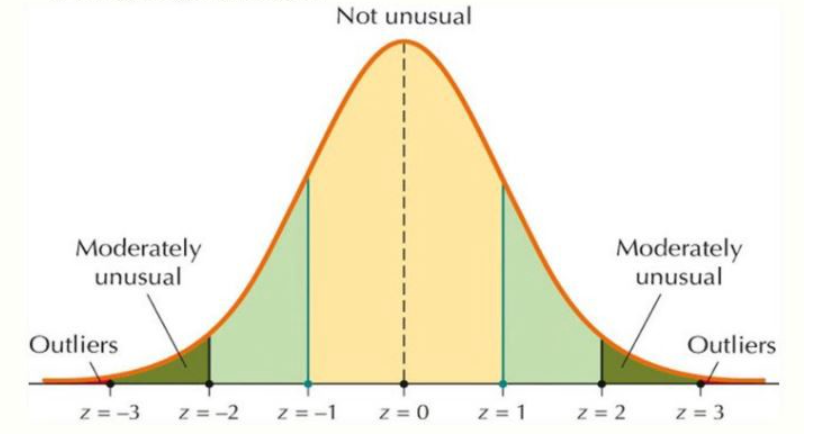
 class ZscoreOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, z_threshold: float = 3): self.z_threshold = z_threshold self.lower = None self.upper = None def fit(self, X: pd.Series): mean = X.mean() std = X.std() self.lower = mean - self.z_threshold * std self.upper = mean + self.z_threshold * std return self def transform(self, X): return X.clip(self.lower, self.upper)

Probieren Sie es mit obigem Beispiel aus

clipped_total_rooms2 = ZscoreOutlierClipper().fit_transform(df_housing["total_rooms"]) clipped_total_rooms2.hist(bins=50);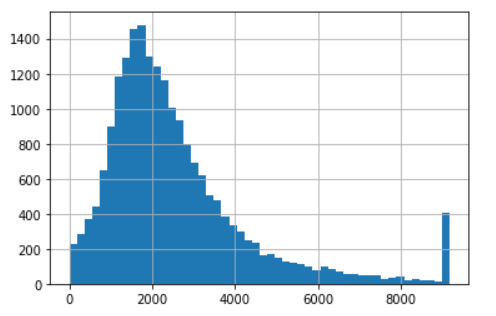

Kommentar:

• Im Vergleich zum Boxplot gibt der Z-Score in diesem Fall einen größeren Wertebereich zurück, Werte größer als 9000 gelten als Ausreißer, während die Obergrenze des Boxplots nur etwa 6000 beträgt.
• Wenn die Ausnahmebehandlung für den Z-Score die Erwartung und die Standardabweichung verschieben kann, ändern sich auch die oberen und unteren Grenzen. Das heißt, die nächste Bestimmung wird sich von der aktuellen unterscheiden.
• Was die IQR anbelangt, so wirkt sich dies unabhängig von den Ausreißern nicht auf die Ober- und Untergrenze aus, da sie nur die Ausreißer in die Ober- oder Untergrenze ersetzen muss.

Die Art und Weise, wie Ausreißer identifiziert und behandelt werden, ist kategorisch.

Im Gegensatz zu numerischen Daten sind Ausreißerdaten in kategorialen Feldern schwieriger zu identifizieren. Teilweise ist es schwierig, Histogramme darzustellen, und die Identifizierung von Ausreißern erfordert spezielles Wissen.

• Mit Wert Ausnahme kann in einem der folgenden Fälle auftreten:
• Aufgrund der unterschiedlichen Eingabemethode. Zum Beispiel die Namen von Städten, also müssen wir sie in eine normalisierte Form zurückbringen, um Ausreißer leicht zu eliminieren.
• Oder es könnte ein Tippfehler sein, für die Verarbeitung können wir ein Histogramm zeichnen, das die Häufigkeit jedes Werts in den gesamten Daten zeigt. Normalerweise sind die Rechtschreibfehler gering.
• Bei einigen Daten, die sich auf Etikettendaten beziehen, die viele unterschiedliche Daten enthalten, die nur schwer auf einen Nenner gebracht oder gekennzeichnet werden können, können wir sie in neue Elemente gruppieren, die etwas gemeinsam haben. Zum Beispiel: Name der Hausnummer, dann können wir feststellen, ob dieses Haus in einer Ecke, in einer Gasse oder an einer großen Straße liegt, um den Hauspreis zu ermitteln.

Zusammenfassung:

Dieser Artikel hat die Identifizierung von Ausreißern bei numerischen oder Katalogdaten und deren Verarbeitung mit zwei Methoden erwähnt: IQR- oder Z-Score.