Die Begriffe Normalverteilung, Exponentialverteilung, hypergeometrische Verteilung, … müssen uns sehr vertraut sein. Aber wie kann man in der Microsoft Excel-Umgebung schneller rechnen?

Mit der vollen Unterstützung von Excel-Funktionen kommen Sie schnell zu den gewünschten Ergebnissen. Und der folgende Artikel wird weitere Details zu den Funktionen in der Distribution vorstellen.

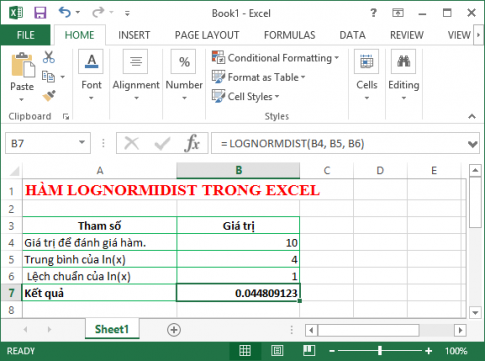
Erste . LOGNORMIDIST .-Funktion

• Funktion: ist eine Funktion, die die kumulative logarithmische Normalverteilung eines bestimmten x-Werts zurückgibt, wobei ln(x) mit dem Mittelwert des Parameters und der Standardabweichung normalverteilt ist. Diese Funktion wird häufig auf die log-transformierte Datenanalyse angewendet.

• Syntax: LOGNORMVERT(x, Mittelwert, Standard_dev)

• Verwendung:

x: ist der Wert zur Auswertung der Funktion

Mittelwert: ist der Durchschnitt von ln(x)

standard_dev: ist die Standardabweichung von ln(x)

• Beispiel: Der Wert zur Auswertung der Funktion ist 10, der Mittelwert von ln(x) ist 4 und die Standardabweichung von ln(x) ist 1:

Aufmerksamkeit:

• Wenn eine Zahl vorhanden ist, die kein Argument ist, gibt die Funktion den #WERT!
• Wenn x oder Standardabweichung <1, gibt die Funktion die #NUM!

2 . EXPONDIST .-Funktion

• Funktion: gibt das Ergebnis einer Exponentialverteilung zurück, diese Funktion wird hauptsächlich verwendet, um die Zeit zwischen Ereignissen abzutasten

• Syntax: Expondist(x,lambda,kumulativ)

• Verwendung:

x: ist der Wert der Funktion

Lambda: ist der Parameterwert

kumulativ: ein logischer Wert, der angibt, welcher Exponentialtyp bereitgestellt werden soll

• Beispiel: Angesichts der tatsächlichen Werte, die den Parametern der Funktion in den Excel-Zellen entsprechen, mit dem Wert der Funktion 0,5. Der Wert des Parameters ist 12 und die beiden logischen Werte sind TRUE & FALSE
• Mit dem logischen Wert TRUE

• Mit einem logischen Wert von FALSE

3 . HYPGEOMVERT .-Funktion

• Funktion: Funktion, die einen hypermultiplen Bruch zurückgibt. Wir verwenden diese Funktion häufig für Probleme mit endlichen Mengen, bei denen jede Beobachtung erfolgreich oder fehlgeschlagen sein kann und in jeder Teilmenge bekannter Größe mit gleicher Fähigkeit ausgewählt werden kann.

• Syntax: HYPGEOMDIST(Probe_s,Anzahl_Probe,Population_s,Anzahl_Pop)

• Verwendung:

Sample_s: Anzahl der Erfolge im Sample

number_sample: Größe der Stichprobe

population_s: Anzahl der Erfolge im Set

number_pop: Größe der Menge

• Beispiel: Gegeben ist der tatsächliche Wert, der dem Parameter der Funktion HYPGEOMVERT entspricht. In diesem Beispiel berechnen wir mit: Anzahl der Erfolge in der Stichprobe ist 5, Stichprobengröße ist 7, Anzahl der Erfolge in der Menge ist 15 und Menge der Menge ist 20:

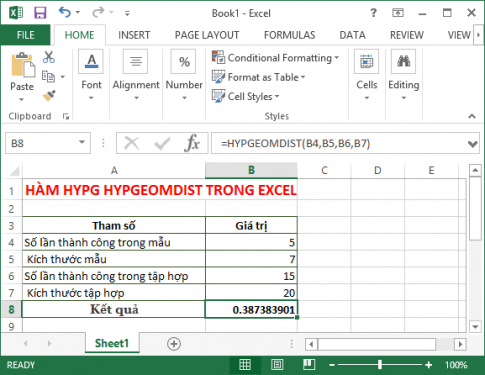
Hinweis :

• Alle Argumente werden auf ganze Zahlen gekürzt.
• Ein nicht numerisches Argument ist vorhanden, die Funktion gibt den Fehler #WERT zurück!.
• Wenn sample_s, number_sample, folk_s, number_population < 1, gibt die Funktion den Fehler #NUM!
• Wenn number_sample > number_population, civil_s > number_population, gibt die Funktion den Fehler #NUM!

Viel Glück!