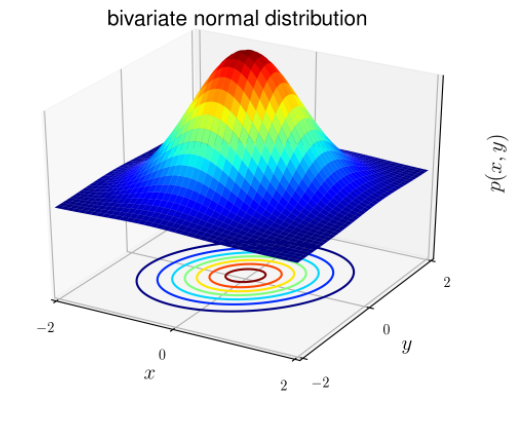
La distribuzione normale è anche nota come distribuzione gaussiana (a campana). La distribuzione ha la stessa forma generale, solo il parametro di posizione (media μ) e il rapporto (varianza σ ² ) sono diversi.

La distribuzione gaussiana ha la forma:

Lì dentro:

• Vettore medio (previsto): μ ∈ R ^d
• Matrice di covarianza : ∈ R ^dxd

Per problemi di classificazione, x è noto per essere casuale continuo (quando x è continuo, i suoi possibili valori riempiono un intervallo sulla retta numerica X ∈ (x _min ; x _max ). Possiamo usare il modello Gaussian Discriminant Analysis (GDA) : predire la probabilità P(x|y) sulla base di una distribuzione normale di molte variabili.

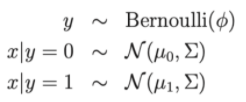
Scrivi come distribuzione:

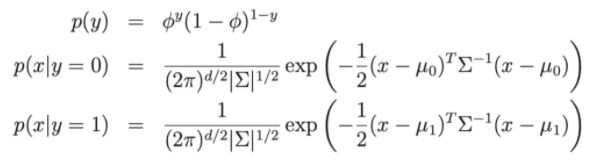
Lì dentro:

• Parametri del modello , , μ ₀ , μ ₁ .
• μ ₀ , μ ₁ sono i due vettori medi di x|y = 0 e x|y = 1
• La funzione di perdita del modello: Log-linkihood

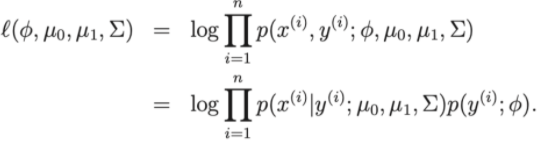
Quindi, per polarizzare la funzione di perdita, possiamo ridurre il problema a trovare i parametri , , μ ₀ , μ ₁ del set di dati di addestramento.

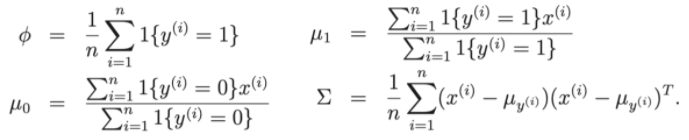
Discutiamo alcuni problemi tra GDA e regressione logistica.

Supponiamo di considerare p(y=1 | ∅, Σ , μ ₀ , μ ₁ ) è una funzione di x, quindi l'espressione avrà ora la forma:

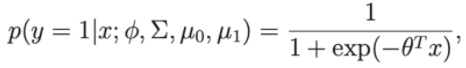
Dove theta è un'approssimazione di , , μ ₀ , μ ₁

Quindi vediamo che ha la stessa forma dell'algoritmo di regressione logistica.

• Quindi se la distribuzione di p(x | y) ha una distribuzione gaussiana, allora il GDA è buono
• Se la distribuzione di p(x | y) non è gaussiana, GDA potrebbe essere meno efficiente.

Algoritmo di classificazione Naive Bayes

Supponiamo che un algoritmo classifichi i clienti o classifichi le email come spam o non spam. Se rappresentiamo l'e-mail come un vettore di funzionalità con dimensioni uguali alla dimensione del dizionario. Se nell'e-mail c'è la j-esima parola nel dizionario, allora x _j = 1 altrimenti x _j = 0. E se l'insieme dei punti delle parole fosse composto da 5000 parole, x ∈ {0, 1} ⁵⁰⁰⁰ . Quindi, se vuoi costruire un classificatore, hai bisogno di almeno 2 ^(50000-1) parametri e non è un numero piccolo.

Per modellare p(x | y) assumiamo che xi sia indipendente. Questa ipotesi è chiamata Naive Bayes (ingenuo). Il risultato dell'algoritmo è il classificatore Naive Bayes.

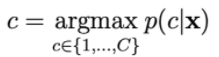
La probabilità p(c | x) è calcolata da:

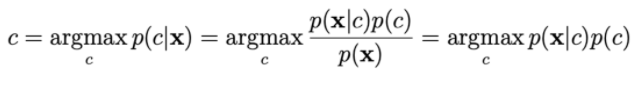
Per calcolare p(x|c), ci basiamo sull'assunto che xi sia indipendente da

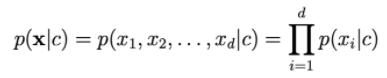
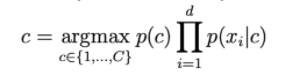
Maggiore è d, minore è la probabilità di ohari. Quindi dobbiamo ottenere il registro sul lato destro per ridimensionarlo.

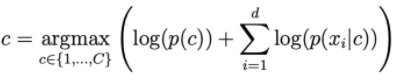
Distribuzioni comunemente usate in NBC.

1. Bayes ingenuo guassiano:

Per ogni dimensione di dati i e una classe c, xi segue una distribuzione normale con μ _ci attesi e varianza σ _ci ² .

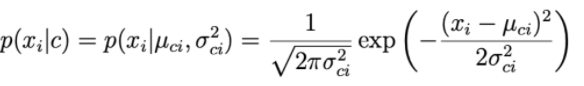
Il parametro μ _ci e la varianza σ _ci ² sono determinati in base ai punti del traning set di classe c.

2. Bernoulli Naive Bayes

Le componenti del vettore delle caratteristiche sono variabili discrete che assumono il valore 0 o 1: Quindi p(xi|c) è calcolato da:

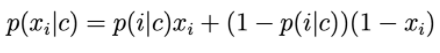
p(i|c) può essere inteso come la probabilità che la parola i appaia nel testo della classe c.

3. Bayes ingenuo multinomiale:

Le componenti del vettore delle caratteristiche sono variabili discrete secondo la distribuzione di Poisson.

Si supponga un problema di classificazione del testo in cui x è una rappresentazione dell'arco.

Il valore dell'i-esimo elemento in ogni vettore è il numero di volte in cui l'i-esima parola ricorre nel testo.

Allora, p(xi|c) è proporzionale alla frequenza con cui la parola i compare nei documenti della classe c.

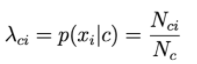
N _ci è il numero totale di volte che appaio nei documenti di classe c.

Nc è il numero totale di parole (compresa la ripetizione) che compaiono nella classe c.

4. Levigatura Laplace.

Se c'è una parola che non compare mai nella classe c, allora la probabilità di andare a destra della seguente formula sarà = 0.

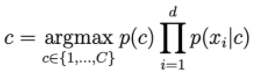
Per risolvere questo problema, viene applicata una tecnica chiamata levigatura di Laplace:

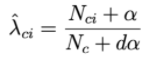
Dove α è un numero positivo, di solito α sarà uguale a 1, il campione più dα aiuta a garantire la probabilità totale. Pertanto, ogni classe c sarà descritta da un sottoinsieme di numeri positivi che si sommano a 1.