I valori anomali o valori anomali sono punti dati diversi dalla panoramica del set di date. Supponiamo che il valore dell'età sia negativo o che un paese non sia elencato sulla mappa. Possiamo utilizzare completamente alcune funzioni in Python per determinare i valori anomali.

Esempio di valori anomali : supponiamo che una classe abbia 100 studenti di cui 99 ottengono 4 punti e l'altro ottiene 10 punti. In un'altra classe tutti nella classe hanno ottenuto 6 punti. Quindi, se vuoi valutare quale classe è migliore, devi determinare la media di ogni studente in ogni classe. Ovviamente, se si calcola il punteggio totale, la classe A ha un punteggio più alto, ma in realtà la classe B è migliore.

Alieni nell'apprendimento automatico

Quando i dati hanno valori anomali, influiranno sicuramente sulla qualità del modello. Dai un'occhiata all'esempio qui sotto:

Esiste un set di dati standard contenente l'altezza e il peso di ogni persona e un set di dati contenente alcuni valori anomali.

importa panda come pd
df_example = pd.DataFrame(
    dati={
        "altezza": [147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "peso": [49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
        "altezza_2": [110, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "peso_2": [49, 90, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
  } ) df_example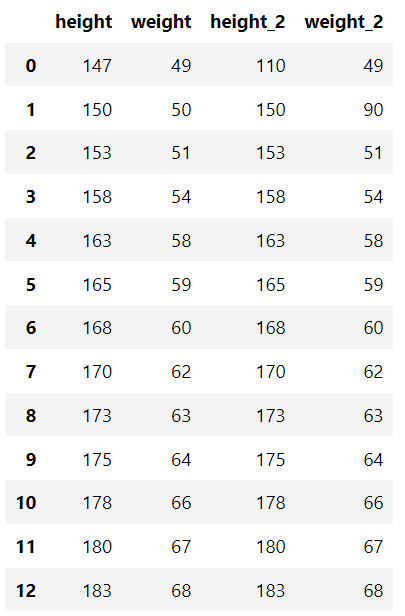

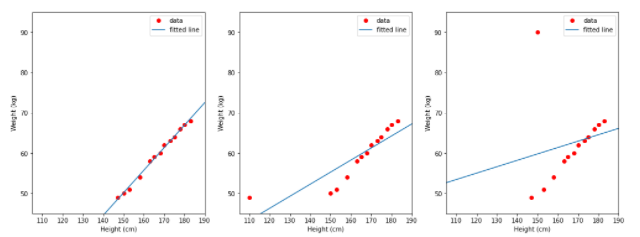
Osservando i dati sopra, si può vedere che altezza e peso sono direttamente proporzionali, il che significa che più alto è un ragazzo, più pesante sarà. Forse il modello di regressione lineare si adatterà a questi dati. Consideriamo 3 casi per determinare i risultati del modello lineare.

• TH1 (a sinistra): utilizza i dati nella colonna altezza come input, nella colonna peso come etichetta.
• TH2 (medio): utilizza i dati nella colonna height_2 come input, nella colonna del peso come etichetta.
• TH3 (destra): usa i dati nella colonna altezza come input, nella colonna weight_2 come etichetta.

 from matplotlib import pyplot as plt from sklearn.linear_model import LinearRegression
def fit_linear_regression_and_visualize( df: pd.DataFrame, input_col: str, label_col: str ): # fit the model by Linear Regression lin_reg = LinearRegression(fit_intercept= True ) lin_reg.fit(df[[input_col]], df[label_col]) w1 = lin_reg.coef_ w0 = lin_reg.intercept_ # visualize plt.plot(df[input_col], df[label_col], "ro", label="data") plt.axis([105, 190, 45, 75]) plt.xlabel("Height (cm)") plt.ylabel("Weight (kg)") plt.ylim(45, 95) plt.plot([105, 190], [w1 * 105 + w0, w1 * 190 + w0], label="fitted line") plt.legend() plt.figure(figsize=(17, 6)) plt.subplot(1, 3, 1) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight") plt.subplot(1, 3, 2) fit_linear_regression_and_visualize(df_example, input_col="height_2", label_col="weight") plt.subplot(1, 3, 3) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight_2")

La linea blu è la linea che il modello ha imparato. Osservando le 3 immagini sopra, possiamo vedere che la figura a sinistra della linea è abbastanza coerente con i dati. Pertanto, c'è un semplice commento sul fatto che i dati anomali nell'input del modello o nell'etichetta di output influiscono sulla correttezza del modello.

Come identificare e gestire i valori anomali che sono numeri.

Esistono 2 tipi principali di valori anomali:

• I valori non sono nell'intervallo specificato dei dati. Ad esempio, età, punteggio o distanza non possono essere negativi.
• È probabile che il valore si realizzi, ma la probabilità è molto bassa. Ad esempio, uno studente che fa il test 100 volte ottiene 1 punto, ma 1 volta ottiene 10 punti. È probabile che questi valori si verifichino, ma sono davvero rari.

Come gestire :

• Con i dati nel primo gruppo, possiamo sostituirlo con nan e considerare quel valore mancante e procedere alla sua elaborazione nella fase di elaborazione dei dati mancanti.
• Per i dati nel secondo gruppo, di solito viene utilizzato il metodo del limite superiore o inferiore (clipping o capping). Cioè, un valore è troppo grande o troppo piccolo, lo portiamo al valore massimo o minimo, che è considerato un punto che non è nel valore anomalo. Ad esempio, se c'è una città in longitudine e latitudine al di fuori dei limiti della mappa, possiamo considerarla in termini di latitudine e longitudine ad essa più vicine e nessuna eccezione. (Puoi usare Python per determinare l'intervallo di eccezioni.)

Metodo IQR.

Per illustrare come utilizzare il box plot, utilizzeremo il set di dati California Housing.

import pandas as pd housing_path ="https://media.githubusercontent.com/media/tiepvupsu/tabml_data/master/california_housing/" df_housing = pd.read_csv(housing_path + "housing.csv") df_housing.head()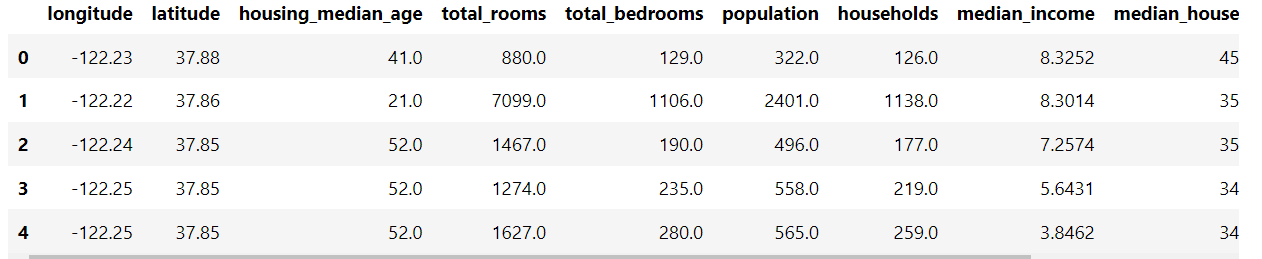

Di seguito è riportato l'istogramma e il box plot della colonna total_rooms

import matplotlib.pyplot as plt fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5)) df_housing[["total_rooms"]].hist(bins=50, ax=axes[0]); df_housing[["total_rooms"]].boxplot(ax=axes[1], vert= False );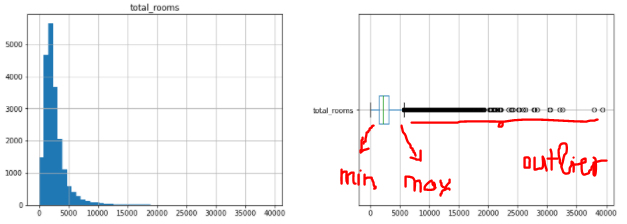

Vediamo nella figura che ci sono non pochi valori sporadici verso destra. Quindi dobbiamo portarli al valore minimo o massimo di Boxplot. Qui uso l'API sklearn per farlo.

from typing import Tuple from sklearn.base import BaseEstimator, TransformerMixin def find_boxplot_boundaries( col: pd.Series, whisker_coeff: float = 1.5 ) -> Tuple[float, float]: """Findx minimum and maximum in boxplot. Args: col: a pandas serires of input. whisker_coeff: whisker coefficient in box plot """ Q1 = col.quantile(0.25) Q3 = col.quantile(0.75) IQR = Q3 - Q1 lower = Q1 - whisker_coeff * IQR upper = Q3 + whisker_coeff * IQR return lower, upper class BoxplotOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, whisker_coeff: float = 1.5): self.whisker = whisker_coeff self.lower = None self.upper = None def fit(self, X: pd.Series): self.lower, self.upper = find_boxplot_boundaries(X, self.whisker) return self def transform(self, X): return X.clip(self.lower, self.upper)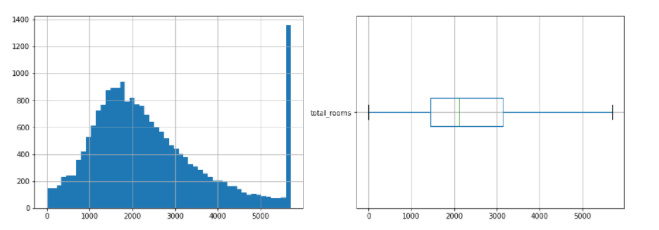

Una piccola spiegazione di cosa significa IQR-Inter Quartile Range usando l'intervallo del quartile medio, determinato da quali valori al di fuori dell'intervallo da -1,5xIQR a 1,5xIQR sono considerati valori anomali.

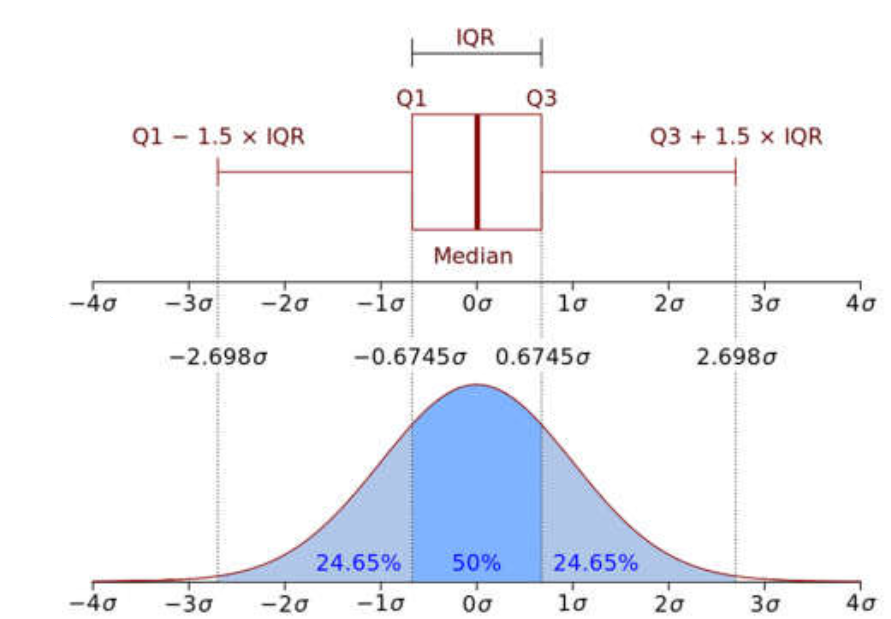
• (Q1–1.5 IQR) rappresenta il valore minimo del set di dati.
• (Q3+1.5 IQR) Rappresenta il valore massimo del set di dati.

Dopo aver suddiviso i dati in base al massimo e al minimo del boxplot, vediamo che i dati sono stati meno distorti. E non vediamo più valori anomali al di fuori del massimo e del minimo.

Il metodo del punteggio Z.

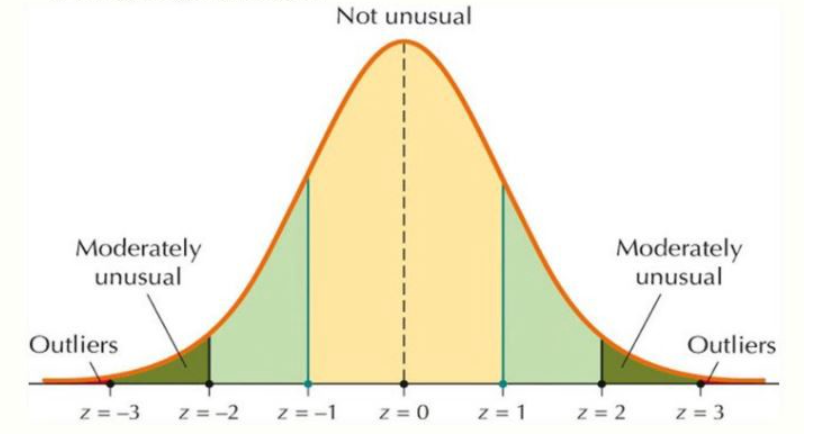
Se i dati seguono una distribuzione normale, puoi applicare la regola 3σ alla distribuzione normale.

In una distribuzione normale, sia μ l'aspettativa e σ la deviazione standard. La regola 3σ per la distribuzione normale dice che:

• Il 68% dei punti dati si trova entro μ±σ
• Il 95% dei punti dati si trova entro μ±2σ
• Il 99,7% dei punti dati si trova entro μ±3σ

Per un punto dati, il suo punteggio z è calcolato da:

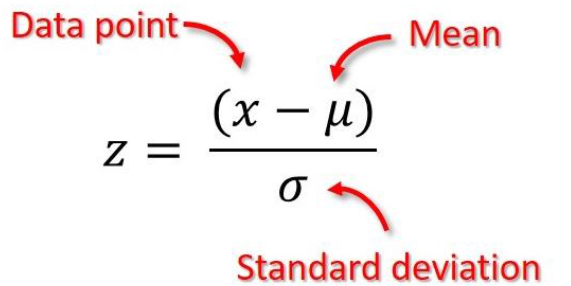
Pertanto, i punti con z-score che possono essere considerati valori anomali sono al di fuori dell'intervallo [-3, 3]. Modificando un po' la matematica, ciò equivale a considerare i punti al di fuori dell'intervallo [μ−3σ,μ+3σ] come valori anomali.

 class ZscoreOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, z_threshold: float = 3): self.z_threshold = z_threshold self.lower = None self.upper = None def fit(self, X: pd.Series): mean = X.mean() std = X.std() self.lower = mean - self.z_threshold * std self.upper = mean + self.z_threshold * std return self def transform(self, X): return X.clip(self.lower, self.upper)

Provalo con l'esempio sopra

clipped_total_rooms2 = ZscoreOutlierClipper().fit_transform(df_housing["total_rooms"]) clipped_total_rooms2.hist(bins=50);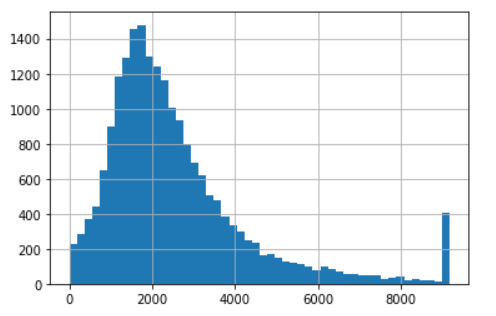

Commento:

• Rispetto al box plot, il punteggio z in questo caso restituisce un intervallo di valori più ampio, valori maggiori di 9000 sono considerati valori anomali mentre il limite superiore del boxplot è solo di circa 6000.
• Quando la gestione delle eccezioni del punteggio z può spostare l'aspettativa e la deviazione standard in modo che anche i limiti superiore e inferiore cambino. Cioè, la prossima determinazione sarà diversa da quella attuale.
• Per quanto riguarda l'IQR, non importa quali siano i valori anomali, non influirà sui limiti superiore e inferiore, perché deve solo sostituire i valori anomali nei limiti superiore o inferiore.

Il modo in cui i valori anomali vengono identificati e gestiti è categorico.

A differenza dei dati numerici, i dati anomali nei campi categoriali sono più difficili da identificare. In parte è difficile tracciare istogrammi e identificare i valori anomali richiede conoscenze specialistiche.

• Con un'eccezione di valore può verificarsi in uno dei seguenti casi:
• A causa della differenza nel metodo di input. Ad esempio, i nomi delle città, quindi dobbiamo riportarli in una forma normalizzata per eliminare facilmente i valori anomali.
• Oppure potrebbe essere un errore di battitura, per l'elaborazione possiamo tracciare un istogramma che mostra la frequenza di ciascun valore nell'intero dato. Di solito gli errori di ortografia saranno bassi.
• Per alcuni dati relativi ai dati dell'etichetta che hanno molti dati diversi difficili da attivare o attivare, possiamo raggrupparli in nuovi elementi che hanno qualcosa in comune. Ad esempio: Nome del numero civico, quindi possiamo determinare se quella casa si trova in un angolo, in un vicolo o in una grande strada da cui determinare il prezzo della casa.

Riepilogo:

Questo articolo ha menzionato l'identificazione di valori anomali sui dati numerici o di catalogo e l'elaborazione degli stessi con due metodi: IQR o punteggio Z.