Rappresentazione binaria intera e operazioni binarie
Il sistema binario (noto anche come sistema di numerazione in base 2) è un sistema di numerazione che utilizza solo due caratteri, 0 e 1, per rappresentare i numeri. raggiunge un valore numerico, questo binario sistema è spesso menzionato quando si impara c, c++, programmazione introduttiva e informatica. Questo articolo ti aiuterà a capire come rappresentare un numero intero in binario ed eseguire operazioni in binario.
Mục lục
1. Rappresentazione decimale in binario:
Veniamo all'esempio di un numero 31 e 33 quando rappresentato in binario come segue:
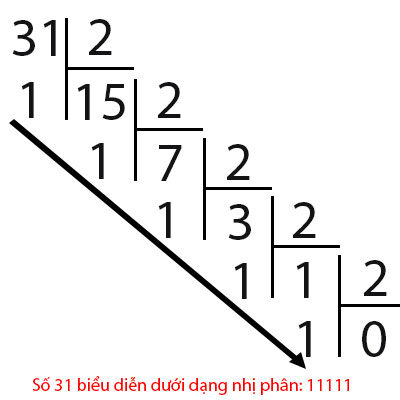
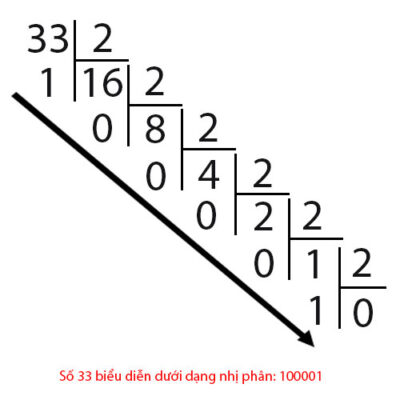
Quindi dai numeri binari, come rappresentare i decimali? Diamo un'occhiata all'esempio seguente:
2. Rappresentazione di numeri binari come decimali
Per ogni unità con valore 1, eseguire il calcolo alla potenza di 2 per 1 volta da destra, ed eseguire il calcolo secondo la seguente formula:
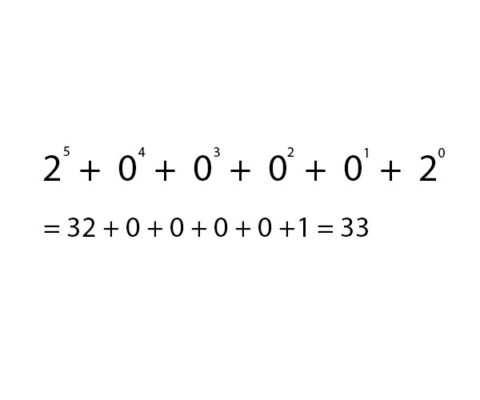
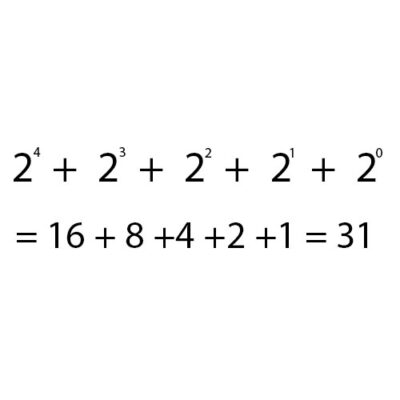
3. Aggiungi 2 numeri binari
Per sommare due numeri binari, applichiamo la regola:
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 (ricorda 1)
Esempio : aggiungi due numeri "1000111" e il numero "11110"
1 0 0 0 1 1 1 (71) + 1 1 1 1 0 (30) ------------- = 1 1 0 0 1 0 1 (101)4. Sottrai 2 numeri binari
Per sottrarre 2 numeri binari, applichiamo la regola:
0 − 0 = 0 0 − 1 = 1 (1 preso in prestito) 1 − 0 = 1 1 − 1 = 0
1 1 0 1 1 1 0 − 1 0 1 1 1 --------------- = 1 0 1 0 1 1 1
5. Rappresentazione di numeri negativi in binario
Prima di entrare nel concetto, puoi leggere questo link come riferimento: https://en.wikipedia.org/wiki/Bi%E1%BB%83u_di%E1%BB%85n_s%E1%BB%91_%C3 %A2m As abbiamo capito, ogni carattere o numeri positivi e negativi nel computer è rappresentato in binario attraverso i numeri 0 e 1, in teoria ci sono molti modi per rappresentare numeri negativi sul computer. Ci interessa come rappresentare il segno di quantità e il complemento a 2. Metodo per rappresentare il segno di quantità: Secondo il principio di rappresentare il segno di quantità, il bit più a sinistra rappresenterà il segno, un byte di 8 bit avrà 7 bit (meno il bit ) . Usando il segno bit, il significato dei 7 bit sopra cambierà e possiamo rappresentare numeri da −127 10 a +127 10 . Nel metodo dei segni, il numero 0 può essere rappresentato in due forme, ovvero 00000000 (+0) e 10000000 (-0).
Tuttavia, questo metodo è facile creare confusione, ad esempio: il numero 143 se convertito in binario, il numero sarà rappresentato come 10001111, ma prova questo programma su c: #include <stdio.h> #include <stdlib.h> void writebitwise(int n){ char buffer [33]; itoa (n,buffer,2); printf ("binary: %sn",buffer); } int main(){ int n = 10; writebitwise(-15); } Il numero -15 sarà rappresentato come una sequenza 11111111111111111111111111111111111110001 (100010001), che è facile da confondere, e quando si eseguono calcoli con numeri binari è abbastanza confusa a causa del segno. Andremo al metodo del complemento a 2 per rappresentare i numeri binari negativi:
- Innanzitutto, il bit del segno è 0 se il numero è positivo e 1 se il numero è negativo.
- In secondo luogo, utilizzare l'operatore bit per bit NOT per invertire tutti i bit di un numero binario positivo (calcolare il bit del segno) per rappresentare il numero negativo corrispondente.
Esempio: il numero 5 10 rappresentato in binario sarebbe 00000101. Il numero −5 10 rappresentato in binario (denominatore a 8 bit) è 11111010. Per rappresentare il complemento a 2, aggiungi 1 al numero binario in complemento a 1, che aggiunge 1 a 11111010: 11111010 + 1 = 11111011. Quindi 11111011 è la rappresentazione in complemento a 2 di −5 10 in un computer.
