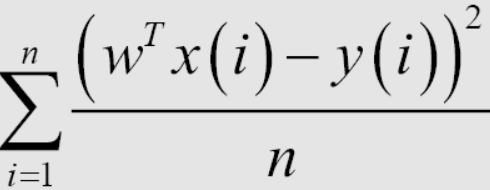
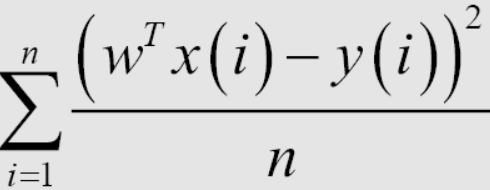
線形回帰モデル
- 24-07-2022
- chuong xuan
- 0 Comments
利用可能なライブラリを使用してモデルをトレーニングしますが、ロックスプーンを使用して、箱の中に何が入っているかを知らずに箱を開けますか?しかし、あなたはまだ箱を開けることができます。アルゴリズム内の理論をよりよく理解すると、パラメーターを使用してモデルを適合させることができます。
このセクションでは、機械学習の最も基本的なアルゴリズムの1つである線形回帰について説明します。このアルゴリズムでは、入力と出力は線形関数によって記述されます。
Mục lục
図解された数学の問題
住宅価格の予測に問題があるとします。その都市には1000戸の家のデータがあり、家という言葉のパラメータは幅がx 1 m2で寝室がx2で、中心から3kmであることがわかっています。上記のパラメータで新しい家を追加すると、家の価格yを予測できますか?はいの場合、予測関数y = f(x)はどのような形式になりますか?ここで、特徴ベクトルx = [x 1、 x 2 、x 3 ] Tは入力情報を含む列ベクトルであり、出力yはスカラーです。
実際、単語の特徴の係数が増加すると、出力も増加するため、単純な線形関数があることがわかります。
y_pre = f(x)= w 0 + w 1 x 1 + w 2 x 2 + … + w n x n = x T w
そこで:
- y_pre:は予測される出力値です。 (そしてy_preは実際のyとは異なります)
- nは特徴の数です。
- (x i )はi番目の機能です
- wはモデルのパラメーターです。ここで、w 0はバイアスであり、パラメーターw 1 、w 2 、…です。
上記の問題は、入力特徴ベクトルに基づいて出力の値を予測する問題です。さらに、出力の値は、多くの異なる正の実数値を取ることができます。したがって、これは回帰の問題です。 y_pre = xTwの関係は線形関係です。線形回帰という名前はここから来ています。
モデルトレーニング
線形回帰モデルを作成した後、モデルのトレーニングは、トレーニングデータセットから最適なパラメーターを見つけることです。これを行うには、モデルが適切かどうかを判断する方法が必要です。ここでは、二乗平均平方根誤差(RMSE)という式を使用することを決定する方法を紹介します。このトレーニングの目標は、平均二乗誤差(MSE)の値を最小化することです。これは単に、予測されたyと実際のyの差をできるだけ小さくしたいということを意味します。
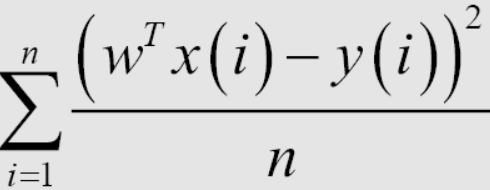
1 / n係数の平均、または損失関数の合計は、問題の解決に数学的な影響を与えません。機械学習では、損失関数には通常、トレーニングセット内の各データポイントの平均係数が含まれているため、テストセットで損失関数の値を計算するときは、各ポイントの平均誤差を計算する必要があります。損失関数を計算すると、データポイントの数が多すぎる場合の過剰適合を回避するのに役立ち、後でモデルを評価するのにも役立ちます。
標準方程式
上記の方程式を最小化するのに役立つwの値を見つけるために、それらがゼロのときのwに関する上方向の導関数を計算できます。そして、最小値を決定します。
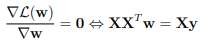
したがって、次の式で最小値を決定できます:w =(X T X) -1XTy 。
ここで、wはMSE(w)が最小化される値です。 yは、(y 1 、… y m )を含む検索ベクトルです。
Pythonで実装します。
以下のデータセットを想定して、身長でその人の体重を決定します。
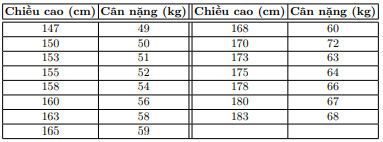
データ表示
import numpy as np
import matplotlib.pyplot as plt
X = np.array([[147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183]]).T
y = np.array([ 49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68])
問題を見て、次の形式のモデルを決定する必要があります:(重量)= w_1 *(高さ)+w_0。
式に従ってソリューションを決定します。
データを初期化する
one = np.ones((X.shape[0], 1)) #Bias
Xbar = np.concatenate((one, X), axis = 1) # each point is one row
次に、式に基づいて係数w_1とw_0を計算します。注:Pythonの行列Aの疑似逆行列は、 numpy.linalg.pinv(A )を使用して計算されます。
A = np.dot(Xbar.T, Xbar)
b = np.dot(Xbar.T, y)
w_best = np.dot(np.linalg.pinv(A), b)
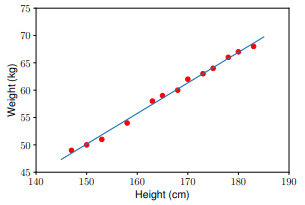
モデルを使用して、テストセットのデータを予測します。
y1 = w_1 * 155 + w_0
y2 = w_1 * 160 + w_0
print('Input 155cm, true output 52kg, predicted output %.2fkg' %(y1) )
print('Input 160cm, true output 56kg, predicted output %.2fkg' %(y2))
結果
Input 155cm, true output 52kg, predicted output 52.94kg
Input 160cm, true output 56kg, predicted output 55.74kg
いくつかのPythonライブラリを試して、結果を比較することもできます。
線形回帰で解決できる問題
式XTWはwとxの両方の線形関数であることがわかります。しかし実際には、線形回帰は、wに関して線形である必要があるモデルにのみ適用できます。例えば:
y w 1 x 1 + w 2 x 2 + w 3 x 2 1 + w 4 sin(x 2 )+ w 5 x 1 x 2 + w 0
はwの線形関数であるため、線形回帰によっても解くことができます。ただし、sin(x2)とx1x2を決定することは比較的不自然です。
線形回帰の制限
線形回帰の最初の制限は、ノイズに非常に敏感であるということです。上記の身長と体重の関係の例では、ノイズの多いデータのペアが1つしかない場合(150 cm、90 kg)、結果は大きく異なります。
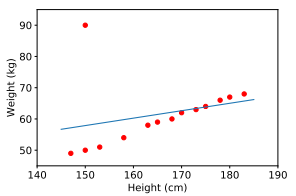
したがって、トレーニングモデルを実装する前に、前のブログで参照できる前処理と呼ばれるステップが必要です。
線形回帰の2番目の制限は、複雑なモデルを表すことができないことです。
まとめ
そのため、この記事では、線形回帰アルゴリズムをトレーニングする方法を紹介しました。基本的に、アルゴリズムをトレーニングするには、次のことが必要です。
- モデルを定義します。
- コスト関数(または損失関数)を定義します。
- トレーニングデータを使用したコスト関数の最適化。
- コスト関数の値が最小であるモデルの重みを見つけます。