外れ値または外れ値は、日付セットの概要とは異なるデータポイントです。年齢の値が負であるか、国がマップにリストされていないとします。 Pythonのいくつかの関数を完全に使用して、外れ値を判別できます。

外れ値の例：クラスに100人の生徒がいて、そのうち99人が4ポイントを獲得し、もう1人が10ポイントを獲得するとします。別のクラスでは、クラスの全員が6ポイントを獲得しました。したがって、どのクラスが優れているかを評価する場合は、各クラスの各生徒の平均を決定する必要があります。明らかに、合計スコアを計算すると、クラスAのスコアが高くなりますが、実際にはクラスBの方が優れています。

機械学習のエイリアン

データに外れ値がある場合、モデルの品質に確実に影響します。以下の例を見てください。

各人の身長と体重を含む標準データセットと、いくつかの外れ値を含むデータセットがあります。

パンダをpdとしてインポートする
df_example = pd.DataFrame（
    data = {
        「高さ」：[147、150、153、158、163、165、168、170、173、175、178、180、183]、
        「重量」：[49、50、51、54、58、59、60、62、63、64、66、67、68]、
        "height_2"：[110、150、153、158、163、165、168、170、173、175、178、180、183]、
        "weight_2"：[49、90、51、54、58、59、60、62、63、64、66、67、68]、
  } ) df_example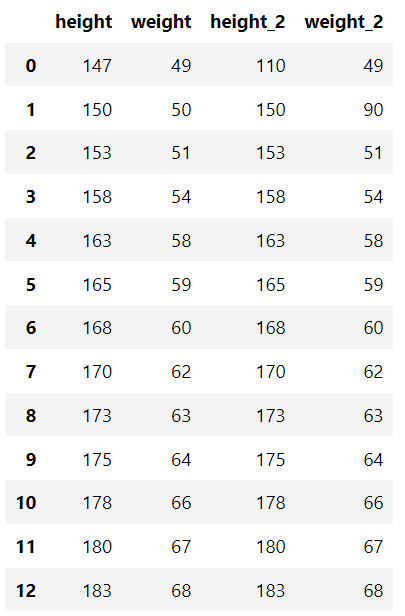

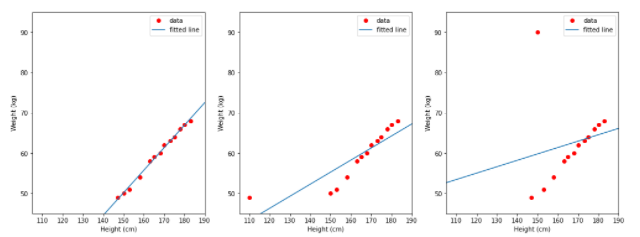
上記のデータを見ると、身長と体重は互いに比例していることがわかります。つまり、男性が背が高いほど、体重が重くなります。おそらく、線形回帰モデルがこのデータに適合します。線形モデルの結果を決定するために、3つのケースを考えてみましょう。

• TH1（左）：高さ列のデータを入力として使用し、重量列のデータをラベルとして使用します。
• TH2（中央）：height_2列のデータを入力として使用し、weight列のデータをラベルとして使用します。
• TH3（右）：height列のデータを入力として使用し、weight_2列のデータをラベルとして使用します。

 from matplotlib import pyplot as plt from sklearn.linear_model import LinearRegression
def fit_linear_regression_and_visualize( df: pd.DataFrame, input_col: str, label_col: str ): # fit the model by Linear Regression lin_reg = LinearRegression(fit_intercept= True ) lin_reg.fit(df[[input_col]], df[label_col]) w1 = lin_reg.coef_ w0 = lin_reg.intercept_ # visualize plt.plot(df[input_col], df[label_col], "ro", label="data") plt.axis([105, 190, 45, 75]) plt.xlabel("Height (cm)") plt.ylabel("Weight (kg)") plt.ylim(45, 95) plt.plot([105, 190], [w1 * 105 + w0, w1 * 190 + w0], label="fitted line") plt.legend() plt.figure(figsize=(17, 6)) plt.subplot(1, 3, 1) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight") plt.subplot(1, 3, 2) fit_linear_regression_and_visualize(df_example, input_col="height_2", label_col="weight") plt.subplot(1, 3, 3) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight_2")

青い線はモデルが学習した線です。上の3つの画像を見ると、線の左側の図がデータと完全に一致していることがわかります。したがって、モデルの入力または出力ラベルの外れ値データがモデルの正確さに影響を与えるかどうかについての簡単なコメントがあります。

数値である外れ値を識別して処理する方法。

外れ値には主に2つのタイプがあります。

• 値がデータの指定された範囲内にありません。たとえば、年齢、スコア、距離を負にすることはできません。
• 値が発生する可能性がありますが、確率は非常に低いです。たとえば、100回テストを受けた学生は1ポイントを獲得しますが、1回は10ポイントを獲得します。これらの値は発生する可能性がありますが、実際にはまれです。

取り扱い方法：

• 最初のグループのデータを使用して、それをnanに置き換え、その値が欠落していると見なして、欠落しているデータ処理ステップで処理に進むことができます。
• 2番目のグループのデータには、通常、上限または下限の方法（クリッピングまたはキャッピング）が使用されます。つまり、値が大きすぎるか小さすぎる場合は、最大値または最小値にします。これは、外れ値にないポイントと見なされます。たとえば、地図の範囲外の経度と緯度に都市がある場合、それに最も近い緯度と経度の観点からそれを考慮することができます。例外はありません。 （Pythonを使用して例外範囲を決定できます。）

IQR法。

箱ひげ図の使用方法を説明するために、CaliforniaHousingデータセットを使用します。

import pandas as pd housing_path ="https://media.githubusercontent.com/media/tiepvupsu/tabml_data/master/california_housing/" df_housing = pd.read_csv(housing_path + "housing.csv") df_housing.head()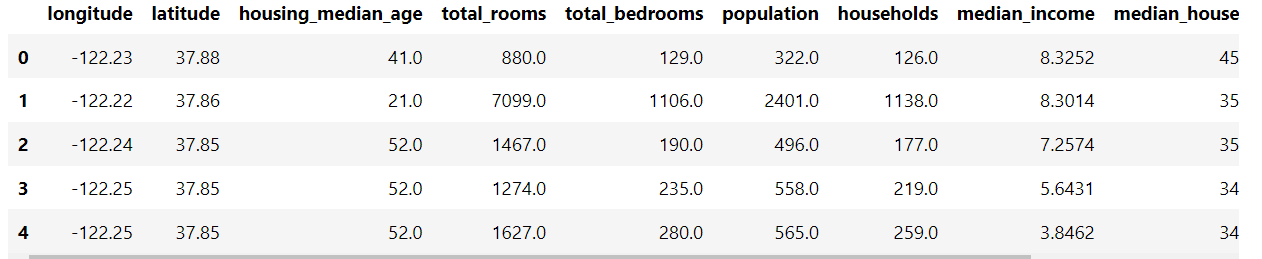

以下は、total_rooms列のヒストグラムと箱ひげ図です。

import matplotlib.pyplot as plt fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5)) df_housing[["total_rooms"]].hist(bins=50, ax=axes[0]); df_housing[["total_rooms"]].boxplot(ax=axes[1], vert= False );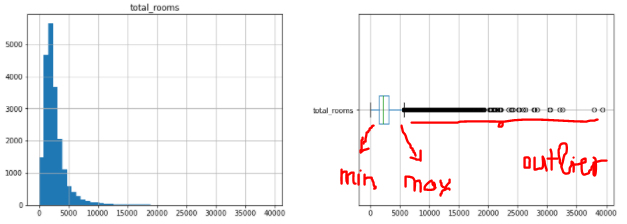

この図では、右側に散発的な値がかなりあることがわかります。したがって、それらをBoxplotの最小値または最大値にする必要があります。ここでは、sklearnAPIを使用してこれを行います。

from typing import Tuple from sklearn.base import BaseEstimator, TransformerMixin def find_boxplot_boundaries( col: pd.Series, whisker_coeff: float = 1.5 ) -> Tuple[float, float]: """Findx minimum and maximum in boxplot. Args: col: a pandas serires of input. whisker_coeff: whisker coefficient in box plot """ Q1 = col.quantile(0.25) Q3 = col.quantile(0.75) IQR = Q3 - Q1 lower = Q1 - whisker_coeff * IQR upper = Q3 + whisker_coeff * IQR return lower, upper class BoxplotOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, whisker_coeff: float = 1.5): self.whisker = whisker_coeff self.lower = None self.upper = None def fit(self, X: pd.Series): self.lower, self.upper = find_boxplot_boundaries(X, self.whisker) return self def transform(self, X): return X.clip(self.lower, self.upper)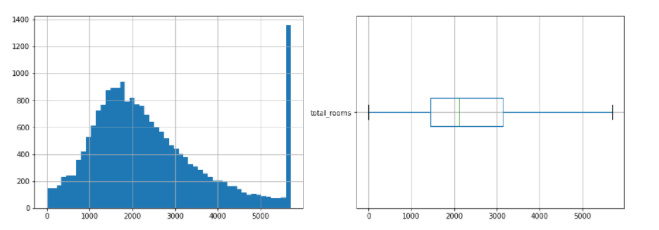

IQR-四分位範囲が中間の四分位範囲を使用することの意味についての簡単な説明。-1.5xIQRから1.5xIQRの範囲外の値が外れ値と見なされるかどうかによって決まります。

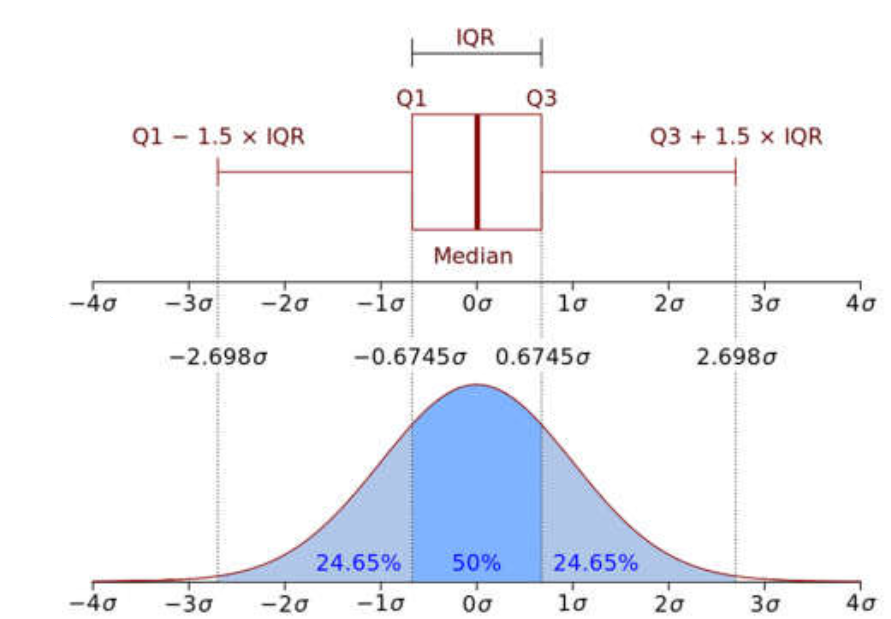
• （Q1–1.5 IQR）は、データセットの最小値を表します。
• （Q3 + 1.5 IQR）データセットの最大値を表します。

箱ひげ図の最大値と最小値に従ってデータをスライスした後、データの偏りが少なくなっていることがわかります。また、最大値と最小値の範囲外の外れ値は表示されなくなりました。

Zスコア法。

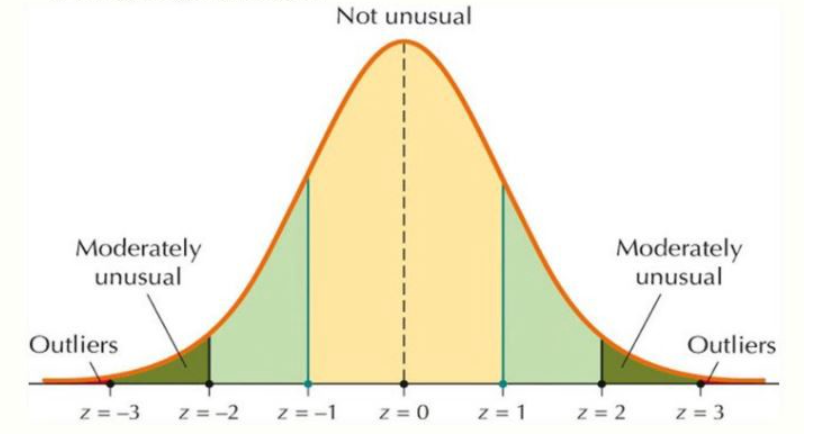
データが正規分布に従う場合は、3σルールを正規分布に適用できます。

正規分布では、μを期待値、σを標準偏差とします。正規分布の3σルールは次のように述べています。

• データポイントの68％がμ±σ以内にある
• データポイントの95％がμ±2σ以内にある
• データポイントの99.7％がμ±3σ以内にある

データポイントの場合、そのzスコアは次のように計算されます。

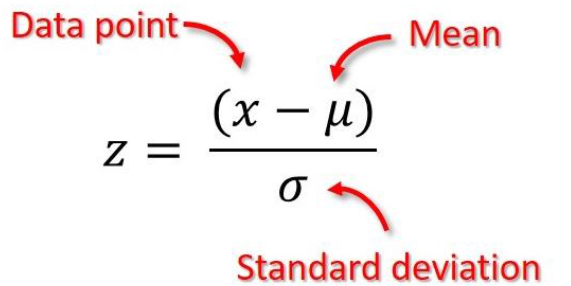
したがって、外れ値と見なすことができるzスコアのあるポイントは範囲外です[-3、3]。計算を少し変更すると、これは、区間[μ-3σ、μ+3σ]の外側の点が外れ値として扱われるのと同じです。

 class ZscoreOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, z_threshold: float = 3): self.z_threshold = z_threshold self.lower = None self.upper = None def fit(self, X: pd.Series): mean = X.mean() std = X.std() self.lower = mean - self.z_threshold * std self.upper = mean + self.z_threshold * std return self def transform(self, X): return X.clip(self.lower, self.upper)

上記の例で試してみてください

clipped_total_rooms2 = ZscoreOutlierClipper().fit_transform(df_housing["total_rooms"]) clipped_total_rooms2.hist(bins=50);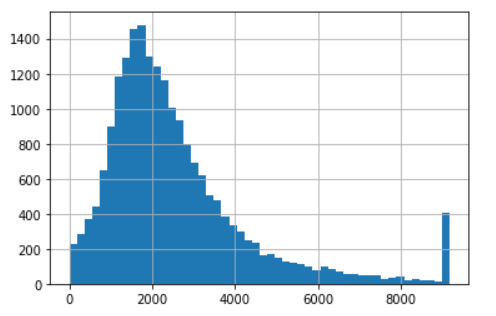

コメント：

• 箱ひげ図と比較して、この場合のzスコアはより広い範囲の値を返し、9000を超える値は外れ値と見なされますが、箱ひげ図の上限は約6000にすぎません。
• zスコアの例外処理により、期待値と標準偏差がシフトする可能性があるため、上限と下限も変更されます。つまり、次の決定は現在の決定とは異なります。
• IQRに関しては、外れ値が何であっても、外れ値を上限または下限に置き換えるだけでよいため、上限と下限には影響しません。

外れ値を識別して処理する方法はカテゴリカルです。

数値データとは異なり、カテゴリフィールドの外れ値データは特定がより困難です。ヒストグラムをグラフ化することは困難であり、外れ値を特定するには専門知識が必要です。

• 値の例外は、次のいずれかの場合に発生する可能性があります。
• 入力方法の違いによる。たとえば、都市の名前なので、外れ値を簡単に削除するには、それらを正規化された形式に戻す必要があります。
• または、タイプミスの可能性があります。処理のために、データ全体の各値の頻度を示すヒストグラムをプロットできます。通常、スペルミスは少なくなります。
• ワンホットまたはエンラブルするのが難しい多くの異なるデータを含むラベルデータに関連する一部のデータについては、共通点がある新しいアイテムにグループ化できます。例：家番号の名前。その家が角にあるのか、路地にあるのか、大通りにあるのかを判断して、そこから住宅価格を決定できます。

概要：

この記事では、数値データまたはカタログデータの外れ値を特定し、IQRまたはZスコアの2つの方法でそれらを処理する方法について説明しました。