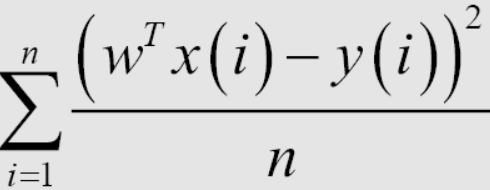
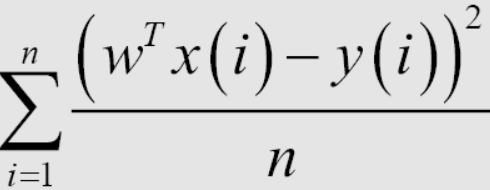
Modelo de regressão linear
- 24-07-2022
- chuong xuan
- 0 Comments
Enquanto usamos as bibliotecas disponíveis para treinar o modelo, mas usamos uma colher de trava para abrir uma caixa sem saber o que tem dentro dela? Mas você ainda pode abrir a caixa. Com uma melhor compreensão das teorias dentro do algoritmo, você pode usar os parâmetros para ajustar o modelo.
Nesta seção, vou familiarizá-lo com a regressão linear, que é um dos algoritmos mais básicos em aprendizado de máquina. Neste algoritmo, a entrada e a saída são descritas por uma função linear.
Mục lục
Problema de matemática ilustrado
Suponha que haja um problema de prever os preços das casas. Há dados de 1000 casas nessa cidade, em que sabemos que os parâmetros na palavra casa é a largura é x 1 m 2 tem x 2 quartos e fica a 3 km do centro. Se você adicionar uma nova casa com os parâmetros acima, poderá prever o preço y da casa? Se sim, de que forma a função preditora y = f(x) se parece? Aqui o vetor de recursos x = [x 1, x 2 , x 3 ] T é um vetor de coluna contendo informações de entrada, a saída y é um escalar.
De fato, podemos ver que, à medida que os coeficientes das características da palavra aumentam, a saída também aumenta, de modo que há uma função linear simples:
y_pre = f(x) = w 0 + w 1 x 1 + w 2 x 2 + … + w n x n = x T w
Lá:
- y_pre: é o valor de saída previsto. (e y_pre será diferente do y real)
- n é o número de recursos.
- (x i ) é a i .ª característica
- w é o parâmetro do modelo onde w 0 é o bias e os parâmetros w 1 , w 2 ,….
O problema acima é o problema de prever o valor da saída com base no vetor de recursos de entrada. Além disso, o valor da saída pode assumir muitos valores reais positivos diferentes. Portanto, este é um problema de regressão. A relação y_pre = x T w é uma relação linear. O nome regressão linear vem daqui.
Treinamento de modelo
Depois de ter um modelo de regressão linear, o treinamento do modelo consiste em encontrar os parâmetros mais ideais por meio do conjunto de dados de treinamento. Para fazer isso, precisamos de uma maneira de determinar se o modelo é bom ou não. Aqui, apresentarei uma maneira de determinar isso usando a expressão Root Mean Square Error (RMSE). O objetivo desse treinamento é minimizar o valor do Erro Quadrado Médio (MSE). Significa simplesmente que queremos que a diferença entre o y previsto e o y real seja a menor possível.
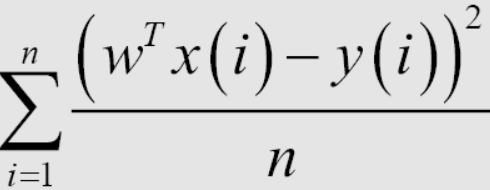
A média 1/n, ou soma na função de perda, matematicamente não afeta a solução do problema. No aprendizado de máquina, as funções de perda geralmente contêm o coeficiente médio para cada ponto de dados no conjunto de treinamento; portanto, ao calcular o valor da função de perda no conjunto de teste, precisamos calcular o erro médio de cada ponto. Calcular a função de perda ajuda a evitar overfitting quando o número de pontos de dados é muito grande e também nos ajuda a avaliar o modelo posteriormente.
Equação Padrão
Para encontrar o valor de w que ajuda a equação acima a atingir seu valor mínimo, podemos calcular a derivada da direção superior em relação a w quando eles são zero. E determine o mínimo.
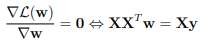
Portanto, podemos determinar o mínimo pela seguinte fórmula: w = (X T X) – 1XTy.
Onde w é o valor no qual MSE(w) é minimizado. y é o vetor a ser encontrado incluindo (y 1 , … y m ).
Implemente em python.
Assumindo o conjunto de dados abaixo, determine o peso dessa pessoa pela altura.
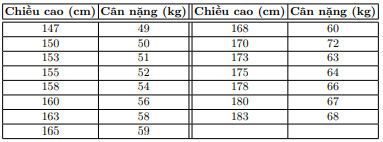
Exibição de dados
import numpy as np
import matplotlib.pyplot as plt
X = np.array([[147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183]]).T
y = np.array([ 49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68])
Olhando para o problema, precisamos determinar o modelo da forma: (peso) = w_1*(altura) + w_0.
Determine a solução de acordo com a fórmula.
Inicializar dados
one = np.ones((X.shape[0], 1)) #Bias
Xbar = np.concatenate((one, X), axis = 1) # each point is one row
Em seguida, calcularemos os coeficientes w_1 e w_0 com base na fórmula . Nota: o pseudo-inverso de uma matriz A em Python será calculado usando numpy.linalg.pinv(A ).
A = np.dot(Xbar.T, Xbar)
b = np.dot(Xbar.T, y)
w_best = np.dot(np.linalg.pinv(A), b)
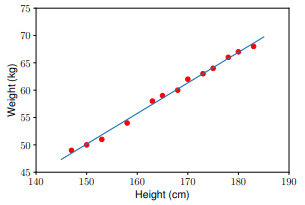
Use o modelo para prever os dados no conjunto de teste:
y1 = w_1 * 155 + w_0
y2 = w_1 * 160 + w_0
print('Input 155cm, true output 52kg, predicted output %.2fkg' %(y1) )
print('Input 160cm, true output 56kg, predicted output %.2fkg' %(y2))
Resultado
Input 155cm, true output 52kg, predicted output 52.94kg
Input 160cm, true output 56kg, predicted output 55.74kg
Você também pode tentar com algumas bibliotecas python para comparar os resultados.
Problemas que podem ser resolvidos por regressão linear
Vemos que a fórmula X T W é uma função linear de w e x. Mas, na verdade, a regressão linear pode ser aplicada a modelos que só precisam ser lineares em relação a w. Por exemplo:
y w 1 x 1 + w 2 x 2 + w 3 x 2 1 + w 4 sen(x 2 ) + w 5 x 1 x 2 + w 0
É uma função linear de w e, portanto, também pode ser resolvida por regressão linear. No entanto, determinar sen(x2) e x1x2 é relativamente antinatural.
Limitações da regressão linear
A primeira limitação da regressão linear é que ela é muito sensível ao ruído. No exemplo de relação altura-peso acima, se houver apenas um par de dados com ruído (150 cm, 90 kg), os resultados serão muito diferentes.
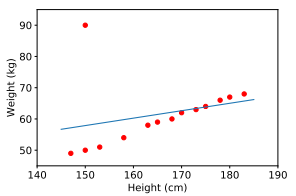
Portanto, antes de implementar o modelo de treinamento, precisamos de uma etapa chamada pré-processamento que falei no blog anterior, que você pode consultar.
A segunda limitação da regressão linear é que ela não pode representar modelos complexos.
resumo
Então, neste artigo, mostrei como treinar um algoritmo de regressão linear. Basicamente, para treinar um algoritmo é necessário:
- Defina o modelo.
- Defina uma função de custo (ou função de perda).
- Otimizando a função de custo usando dados de treinamento.
- Encontre os pesos do modelo onde a função de custo tem o menor valor.