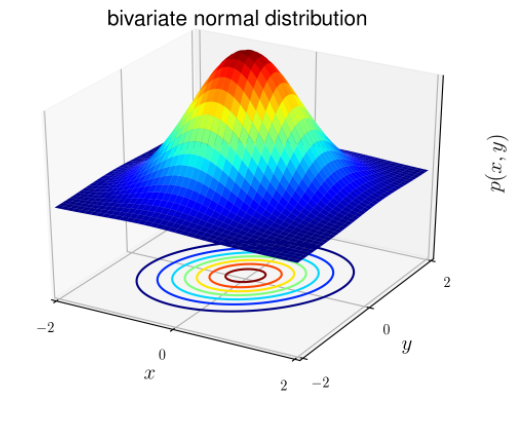
A distribuição normal também é conhecida como distribuição gaussiana (em forma de sino). A distribuição tem a mesma forma geral, apenas o parâmetro de posição (média μ) e a razão (variância σ ² ) são diferentes.

A distribuição gaussiana tem a forma:

Lá:

• Vetor médio (esperado): μ ∈ R ^d
• Matriz de covariância : ∈ R ^dxd

Para problemas de classificação, x é conhecido por ser aleatório contínuo (quando x é contínuo, seus valores possíveis preenchem um intervalo na reta numérica X ∈ (x _min ; x _max ). Podemos usar o modelo de Análise Discriminante Gaussiana (GDA) : prever a probabilidade P(x|y) com base em uma distribuição normal de muitas variáveis.

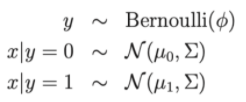
Escreva como uma distribuição:

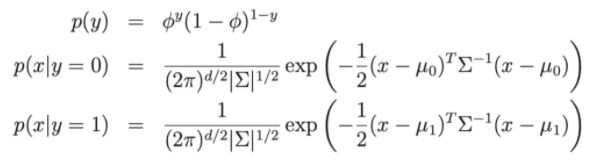
Lá:

• Parâmetros do modelo , , μ ₀ , μ ₁ .
• μ ₀ , μ ₁ são os dois vetores médios de x|y = 0 e x|y = 1
• A função de perda do modelo: Log-linkihood

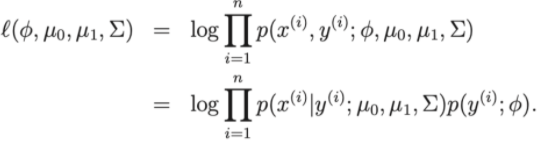
Assim, para pólo na função de perda, podemos reduzir o problema para encontrar os parâmetros , , μ ₀ , μ ₁ do conjunto de dados de treinamento.

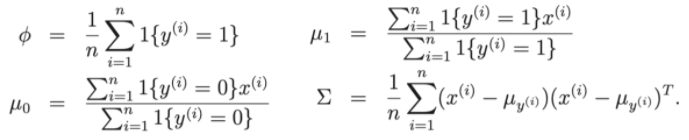
Vamos discutir algumas questões entre GDA e regressão logística.

Suponha que se considerarmos p(y=1 | ∅, Σ , μ ₀ , μ ₁ ) é uma função de x, então a expressão terá agora a forma:

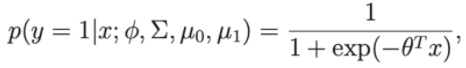
Onde teta é uma aproximação de , , μ ₀ , μ ₁

Assim vemos que tem a mesma forma que o algoritmo de regressão logística.

• Então, se a distribuição de p(x | y) tem uma distribuição gaussiana, então o GDA é bom
• Se a distribuição de p(x | y) não for gaussiana, então GDA pode ser menos eficiente.

Algoritmo classificador Naive Bayes

Suponha que um algoritmo classifique clientes ou classifique e-mails como spam ou não spam. Se representarmos o email como um vetor de recursos com dimensões iguais ao tamanho do dicionário. Se no e-mail houver a jª palavra no dicionário então x _j = 1 caso contrário x _j = 0. E se o conjunto de pontos de palavras consistir em 5000 palavras, x ∈ {0, 1} ⁵⁰⁰⁰ . Portanto, se você deseja construir um classificador, precisa de pelo menos 2 ^(50000-1) parâmetros e esse não é um número pequeno.

Para modelar p(x | y) assumimos que xi é independente. Essa suposição é chamada Naive Bayes (ingênua). O resultado do algoritmo é o classificador Naive Bayes.

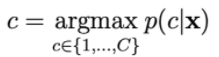
A probabilidade p(c | x) é calculada por:

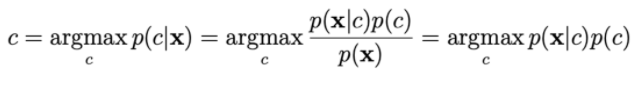
Para calcular p(x|c), contamos com a suposição de que xi é independente de

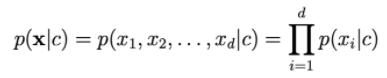
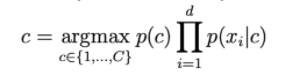
Quanto maior for d, menor será a probabilidade de ohari. Portanto, precisamos obter o log do lado direito para escalá-lo.

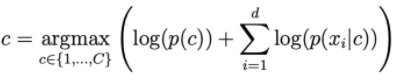
Distribuições comumente usadas na NBC.

1. Bayes ingênuo guassiano:

Para cada dimensão de dados i e uma classe c, xi segue uma distribuição normal com μ _ci esperada e variância σ _ci ² .

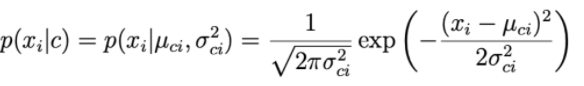
O parâmetro µ _ci e a variância σ _ci ² são determinados com base nos pontos do conjunto de treinamento da classe c.

2. Bernoulli Naive Bayes

Os componentes do vetor de características são variáveis discretas que assumem o valor 0 ou 1: Então p(xi|c) é calculado por:

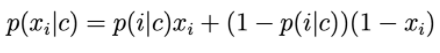
p(i|c) pode ser entendido como a probabilidade de que a palavra i apareça no texto da classe c.

3. Multinomial Naive Bayes:

Os componentes do vetor de características são variáveis discretas de acordo com a distribuição de Poisson.

Suponha um problema de classificação de texto onde x é uma representação Bow.

O valor do i-ésimo elemento em cada vetor é o número de vezes que a i-ésima palavra ocorre no texto.

Então, p(xi|c) é proporcional à frequência com que a palavra i aparece nos documentos da classe c.

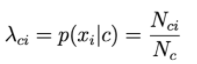
N _ci é o número total de vezes que i aparece nos documentos da classe c.

Nc é o número total de palavras (incluindo repetição) que aparecem na classe c.

4. Alisamento de Laplace.

Se houver uma palavra que nunca aparece na classe c, então a probabilidade de ir para a direita da fórmula a seguir será = 0.

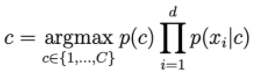
Para resolver isso, uma técnica chamada suavização de Laplace é aplicada:

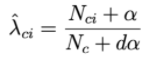
Onde α é um número positivo, geralmente α será igual a 1, a amostra mais dα ajuda a garantir a probabilidade total. Assim, cada classe c será descrita por um subconjunto de números positivos que somam 1.