Outliers ou outliers são pontos de dados que são diferentes da visão geral do conjunto de datas. Suponha que o valor da idade seja negativo ou um país não esteja listado no mapa. Podemos usar completamente algumas funções em python para determinar os outliers.

Exemplo de outliers : Suponha que uma turma tenha 100 alunos, dos quais 99 recebem 4 pontos e o outro recebe 10 pontos. Em outra classe, todos na classe obtiveram 6 pontos. Assim, se você quiser avaliar qual turma é melhor, você precisa determinar a média de cada aluno em cada turma. Obviamente, se a pontuação total for calculada, a classe A tem uma pontuação mais alta, mas, na realidade, a classe B é melhor.

Alienígenas no aprendizado de máquina

Quando os dados têm outliers, isso definitivamente afetará a qualidade do modelo. Dê uma olhada no exemplo abaixo:

Existe um conjunto de dados padrão contendo a altura e o peso de cada pessoa e um conjunto de dados contendo alguns valores discrepantes.

importar pandas como pd
df_example = pd.DataFrame(
    dados={
        "altura": [147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "peso": [49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
        "altura_2": [110, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "peso_2": [49, 90, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
  } ) df_example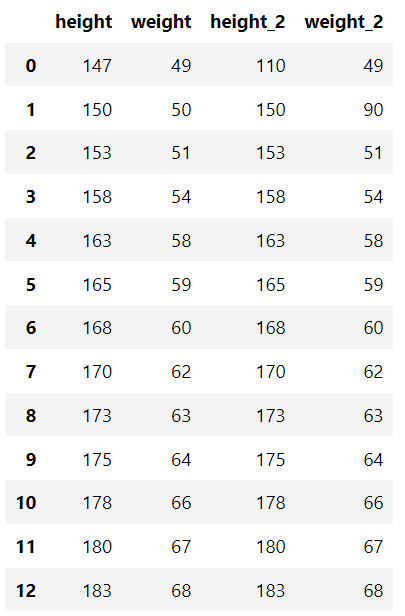

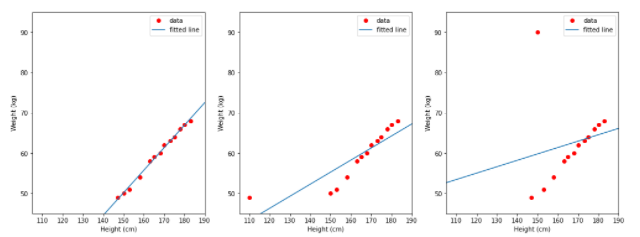
Observando os dados acima, pode-se ver que altura e peso são proporcionais entre si, ou seja, quanto mais alto um cara for, mais pesado ele será. Talvez o modelo de regressão linear se ajuste a esses dados. Vamos considerar 3 casos para determinar os resultados do modelo linear.

• TH1 (esquerda): use os dados na coluna de altura como entrada, na coluna de peso como rótulo.
• TH2 (meio): usa os dados na coluna height_2 como entrada, na coluna de peso como rótulo.
• TH3 (direita): use os dados na coluna de altura como entrada, na coluna peso_2 como rótulo.

 from matplotlib import pyplot as plt from sklearn.linear_model import LinearRegression
def fit_linear_regression_and_visualize( df: pd.DataFrame, input_col: str, label_col: str ): # fit the model by Linear Regression lin_reg = LinearRegression(fit_intercept= True ) lin_reg.fit(df[[input_col]], df[label_col]) w1 = lin_reg.coef_ w0 = lin_reg.intercept_ # visualize plt.plot(df[input_col], df[label_col], "ro", label="data") plt.axis([105, 190, 45, 75]) plt.xlabel("Height (cm)") plt.ylabel("Weight (kg)") plt.ylim(45, 95) plt.plot([105, 190], [w1 * 105 + w0, w1 * 190 + w0], label="fitted line") plt.legend() plt.figure(figsize=(17, 6)) plt.subplot(1, 3, 1) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight") plt.subplot(1, 3, 2) fit_linear_regression_and_visualize(df_example, input_col="height_2", label_col="weight") plt.subplot(1, 3, 3) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight_2")

A linha azul é a linha que o modelo aprendeu. Observando as 3 imagens acima, podemos ver que a figura à esquerda da linha é bastante consistente com os dados. Assim, há um comentário simples de que se os dados discrepantes na entrada do modelo ou no rótulo de saída afetam a correção do modelo.

Como identificar e lidar com valores discrepantes que são números.

Existem 2 tipos principais de outliers:

• Os valores não estão no intervalo especificado dos dados. Por exemplo, idade, pontuação ou distância não podem ser negativas.
• É provável que o valor aconteça, mas a probabilidade é muito baixa. Por exemplo, um aluno que faz o teste 100 vezes ganha 1 ponto, mas 1 vez ganha 10 pontos. Esses valores são prováveis de ocorrer, mas são realmente raros.

Como lidar :

• Com os dados do primeiro grupo, podemos substituí-los por nan e considerar esse valor como ausente e proceder ao processamento na etapa de processamento de dados ausentes.
• Para dados do segundo grupo, geralmente é usado o método de limite superior ou inferior (recorte ou capping). Ou seja, um valor muito grande ou muito pequeno, trazemos para o valor máximo ou mínimo, que é considerado um ponto que não está no outlier. Por exemplo, se houver uma cidade em longitude e latitude fora dos limites do mapa, podemos considerá-la em termos de latitude e longitude mais próxima a ela e sem exceção. (Você pode usar python para determinar o intervalo de exceção.)

método IQR.

Para ilustrar como usar o gráfico de caixa, usaremos o conjunto de dados da California Housing.

import pandas as pd housing_path ="https://media.githubusercontent.com/media/tiepvupsu/tabml_data/master/california_housing/" df_housing = pd.read_csv(housing_path + "housing.csv") df_housing.head()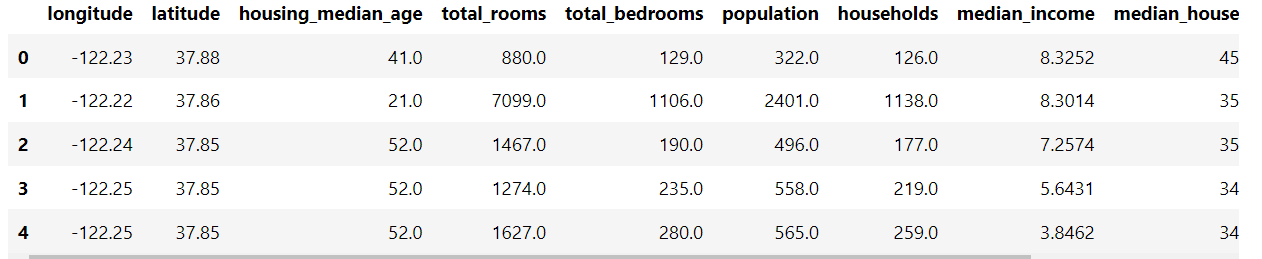

Abaixo está o histograma e o gráfico de caixa da coluna total_rooms

import matplotlib.pyplot as plt fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5)) df_housing[["total_rooms"]].hist(bins=50, ax=axes[0]); df_housing[["total_rooms"]].boxplot(ax=axes[1], vert= False );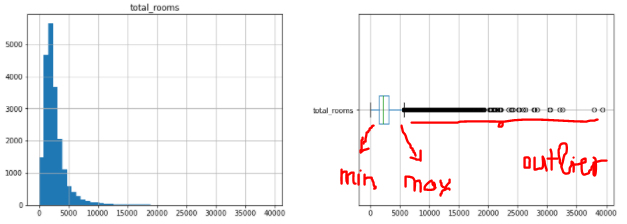

Vemos na figura que existem alguns valores esporádicos para a direita. Portanto, precisamos trazê-los para o valor mínimo ou máximo do Boxplot. Aqui eu uso a API sklearn para fazer isso.

from typing import Tuple from sklearn.base import BaseEstimator, TransformerMixin def find_boxplot_boundaries( col: pd.Series, whisker_coeff: float = 1.5 ) -> Tuple[float, float]: """Findx minimum and maximum in boxplot. Args: col: a pandas serires of input. whisker_coeff: whisker coefficient in box plot """ Q1 = col.quantile(0.25) Q3 = col.quantile(0.75) IQR = Q3 - Q1 lower = Q1 - whisker_coeff * IQR upper = Q3 + whisker_coeff * IQR return lower, upper class BoxplotOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, whisker_coeff: float = 1.5): self.whisker = whisker_coeff self.lower = None self.upper = None def fit(self, X: pd.Series): self.lower, self.upper = find_boxplot_boundaries(X, self.whisker) return self def transform(self, X): return X.clip(self.lower, self.upper)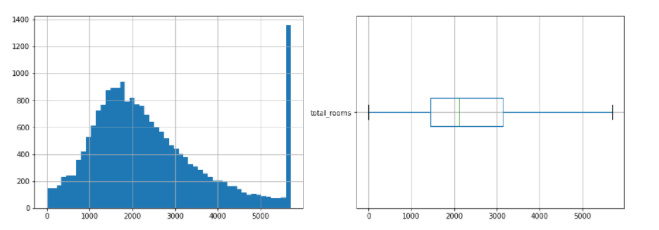

Uma pequena explicação do que significa IQR-Inter Quartile Range usando o intervalo do quartil médio, determinado por quais valores fora do intervalo -1,5xIQR a 1,5xIQR são considerados outliers.

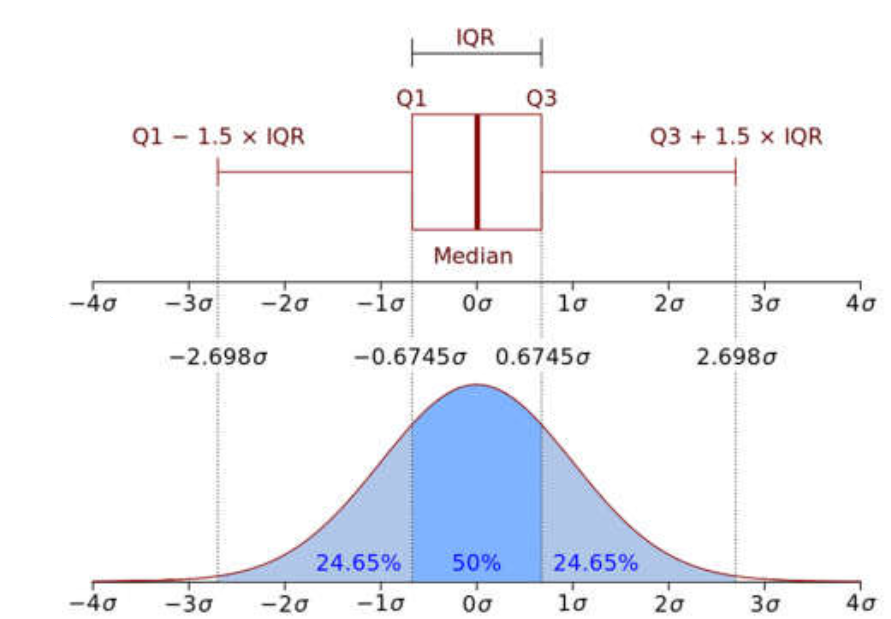
• (Q1–1.5 IQR) representa o valor mínimo do conjunto de dados.
• (Q3+1.5 IQR) Representa o valor máximo do conjunto de dados.

Depois de fatiar os dados de acordo com o máximo e o mínimo do boxplot, vemos que os dados ficaram menos distorcidos. E não vemos mais outliers fora do máximo e do mínimo.

O método de pontuação Z.

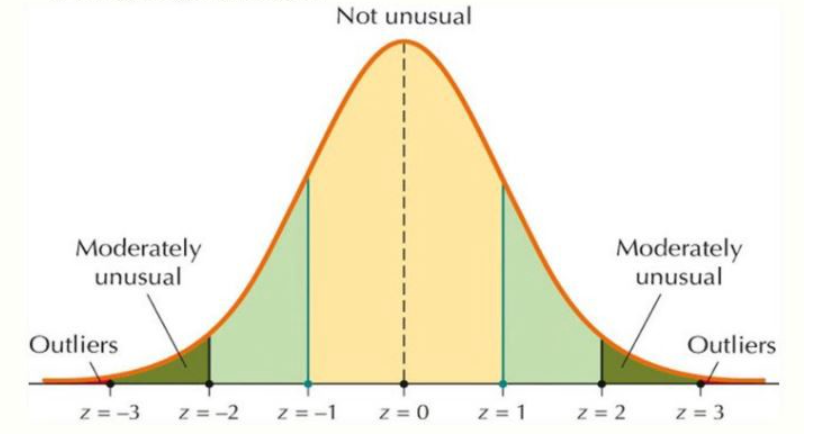
Se os dados seguem uma distribuição normal, você pode aplicar a regra 3σ à distribuição normal.

Em uma distribuição normal, seja μ a expectativa e σ o desvio padrão. A regra 3σ para a distribuição normal diz que:

• 68% dos pontos de dados estão dentro de μ±σ
• 95% dos pontos de dados estão dentro de μ±2σ
• 99,7% dos pontos de dados estão dentro de μ±3σ

Para um ponto de dados, sua pontuação z é calculada por:

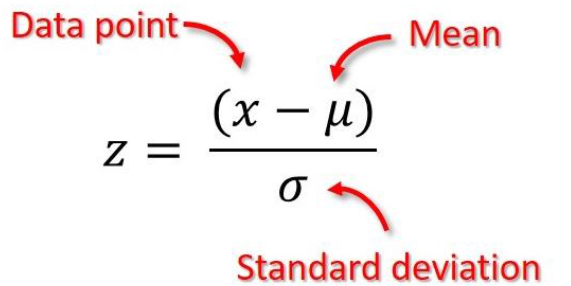
Assim, os pontos com escore z que podem ser considerados outliers estão fora do intervalo [-3, 3]. Mudando um pouco a matemática, isso é equivalente a ter pontos fora do intervalo [μ−3σ,μ+3σ] sendo tratados como outliers.

 class ZscoreOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, z_threshold: float = 3): self.z_threshold = z_threshold self.lower = None self.upper = None def fit(self, X: pd.Series): mean = X.mean() std = X.std() self.lower = mean - self.z_threshold * std self.upper = mean + self.z_threshold * std return self def transform(self, X): return X.clip(self.lower, self.upper)

Experimente com o exemplo acima

clipped_total_rooms2 = ZscoreOutlierClipper().fit_transform(df_housing["total_rooms"]) clipped_total_rooms2.hist(bins=50);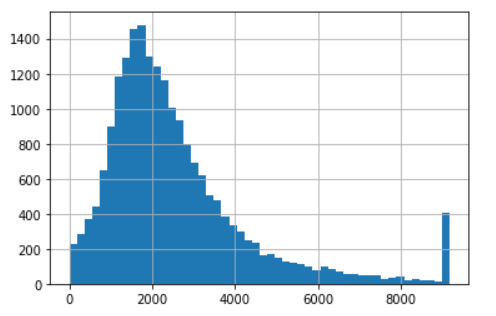

Comente:

• Comparado com o box plot, o z score neste caso retorna uma faixa mais ampla de valores, valores maiores que 9000 são considerados outliers enquanto o limite superior do boxplot é apenas cerca de 6000.
• Como o tratamento de exceção de pontuação z pode alterar a expectativa e o desvio padrão, os limites superior e inferior também serão alterados. Ou seja, a próxima determinação será diferente da atual.
• Quanto ao IQR, não importa quais sejam os valores atípicos, ele não afetará os limites superior e inferior, pois só precisa substituir os valores atípicos nos limites superior ou inferior.

A forma como os outliers são identificados e tratados é categórica.

Ao contrário dos dados numéricos, os dados discrepantes em campos categóricos são mais difíceis de identificar. Parte disso é difícil de traçar histogramas e identificar outliers requer conhecimento especializado.

• Com exceção de valor pode ocorrer em um dos seguintes casos:
• Devido à diferença no método de entrada. Por exemplo, os nomes das cidades, portanto, precisamos devolvê-los a uma forma normalizada para eliminar facilmente os valores discrepantes.
• Ou pode ser um erro de digitação, para processamento podemos traçar um histograma mostrando a frequência de cada valor em todos os dados. Normalmente, os erros de ortografia serão baixos.
• Para alguns dados relacionados aos dados do rótulo que possuem muitos dados diferentes que são difíceis de serem ativados ou ativados, podemos agrupá-los em novos itens que tenham algo em comum. Por exemplo: Nome do número da casa, então podemos determinar se essa casa está em uma esquina, em um beco ou em uma rua grande para determinar o preço da casa.

Resumo:

Este artigo mencionou identificar discrepâncias em dados numéricos ou de catálogo e processá-los por dois métodos: IQR ou pontuação Z.