Representação de inteiros binários e operações binárias
O sistema binário (também conhecido como sistema de numeração de base 2) é um sistema de numeração que usa apenas dois caracteres, 0 e 1, para representar números. atinge um valor numérico, esse binário sistema é frequentemente mencionado ao aprender c, c++, programação introdutória e ciência da computação. Este artigo ajudará você a entender como representar um inteiro em binário e realizar operações em binário.
Mục lục
1. Representação decimal em binário:
Chegamos ao exemplo de um número 31 e 33 quando representado em binário da seguinte forma:
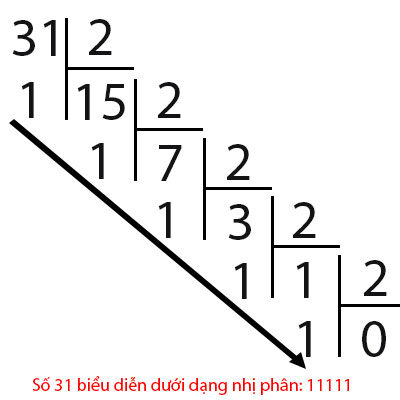
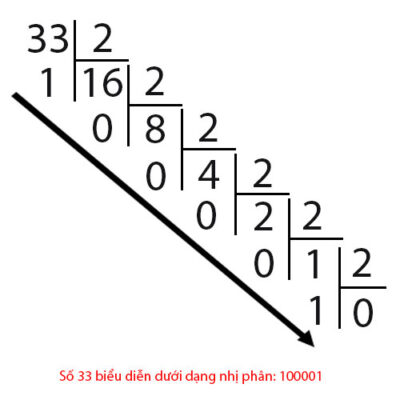
Então, a partir de números binários, como representar decimais? Vamos dar uma olhada no exemplo abaixo:
2. Representando números binários como decimais
Para cada unidade com o valor 1, faça o cálculo à potência de 2 por 1 a partir da direita, e faça o cálculo de acordo com a seguinte fórmula:
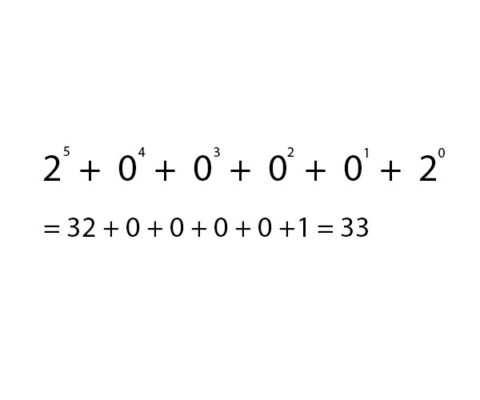
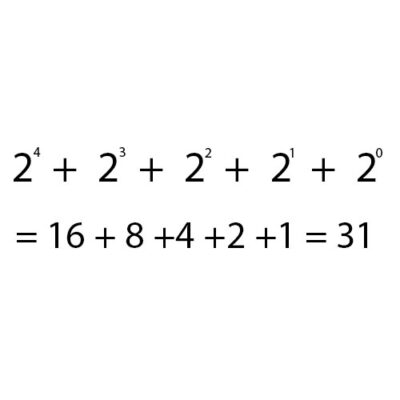
3. Adicione 2 números binários
Para somar dois números binários, aplicamos a regra:
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 (lembre-se de 1)
Exemplo : Adicione dois números "1000111" e o número "11110"
1 0 0 0 1 1 1 (71) + 1 1 1 1 0 (30) ------------- = 1 1 0 0 1 0 1 (101)4. Subtraia 2 números binários
Para subtrair 2 números binários, aplicamos a regra:
0 − 0 = 0 0 − 1 = 1 (1 emprestado) 1 − 0 = 1 1 − 1 = 0
1 1 0 1 1 1 0 − 1 0 1 1 1 --------------- = 1 0 1 0 1 1 1
5. Representando números negativos em binário
Antes de entrar no conceito, você pode ler este link para referência: https://en.wikipedia.org/wiki/Bi%E1%BB%83u_di%E1%BB%85n_s%E1%BB%91_%C3 %A2m As entendemos, todo caractere ou número positivo e negativo no computador é representado em binário através dos números 0 e 1, em teoria, existem muitas maneiras de representar números negativos no computador. Estamos interessados em como representar o sinal de quantidade e o complemento de 2. Método de representação do sinal de quantidade: De acordo com o princípio de representação do sinal de quantidade, o bit mais à esquerda representará o sinal, um byte de 8 bits terá 7 bits (menos o bit). é usado para representar números de 0000000 (0 10 ) a 1111111 (127 10 ). Usando o bit de sinal, o significado dos 7 bits acima mudará e podemos representar números de -127 10 a +127 10 . No método do sinal, o número 0 pode ser representado de duas formas, a saber, 00000000 (+0) e 10000000 (−0).
No entanto, este método é fácil de causar confusão, por exemplo: o número 143 se convertido para binário, o número será representado como 10001111, mas tente este programa em c: #include <stdio.h> #include <stdlib.h> void writebitwise(int n){ char buffer [33]; itoa (n,buffer,2); printf ("binary: %sn",buffer); } int main(){ int n = 10; writebitwise(-15); } O número -15 será representado como uma sequência 1111111111111111111111111110001 (10001111), que é fácil de confundir, e ao fazer cálculos com números binários fica bastante confuso por causa do sinal. Iremos para o método do complemento de 2 para representar números binários negativos:
- Primeiro, o bit de sinal é 0 se o número for positivo e 1 se o número for negativo.
- Segundo, use o operador bit a bit NOT para inverter todos os bits de um número binário positivo (calcular o bit de sinal) para representar o número negativo correspondente.
Exemplo: O número 5 10 representado em binário seria 00000101. O número -5 10 representado em binário (denominador de 8 bits) é 11111010. Para representar o complemento de 2, adicione 1 ao número. binário no complemento de 1, que adiciona 1 a 11111010: 11111010 + 1 = 11111011. Portanto, 11111011 é a representação em complemento de 2 de -5 10 em um computador.
Bài viết liên quan:
Dịch vụ thiết kế Wesbite
