Binary integer representation and binary operations
The binary system (also known as the base 2 numbering system) is a numbering system that uses only two characters, 0 and 1, to represent numbers. reaches a numeric value, this binary system is often mentioned when learning c, c++ , introductory programming and computer science. This article will help you understand how to represent an integer in binary and perform operations in binary.
Mục lục
1. Decimal representation in binary:
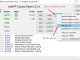
We come to an example of a number 31 and 33 when represented in binary as follows:
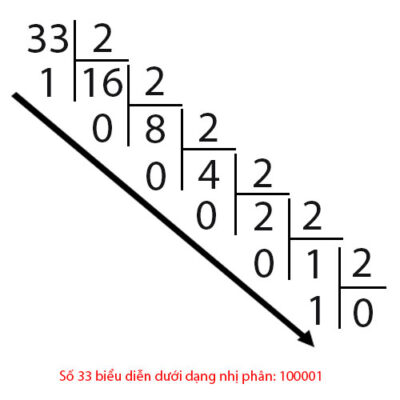
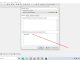
So from binary numbers, how to represent decimals? Let's take a look at the example below:
2. Representing binary numbers as decimals
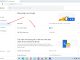
For each unit with the value 1, do the calculation to the power of 2 by 1 time from the right, and do the calculation according to the following formula:
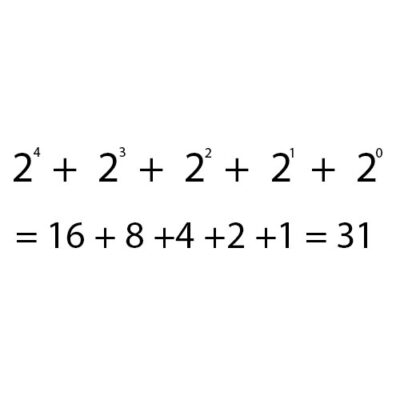
3. Add 2 binary numbers
To add two binary numbers, we apply the rule:
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 (remember 1)
Example : Add two numbers "1000111" and number "11110"
1 0 0 0 1 1 1 (71) + 1 1 1 1 0 (30) ------------- = 1 1 0 0 1 0 1 (101)4. Subtract 2 binary numbers
To subtract 2 binary numbers, we apply the rule:
0 − 0 = 0 0 − 1 = 1 (borrowed 1) 1 − 0 = 1 1 − 1 = 0
1 1 0 1 1 1 0 − 1 0 1 1 1 --------------- = 1 0 1 0 1 1 1
5. Representing negative numbers in binary
Before entering the concept, you can read through this link for reference: https://en.wikipedia.org/wiki/Bi%E1%BB%83u_di%E1%BB%85n_s%E1%BB%91_%C3 %A2m As we have understood, every character or positive and negative numbers in the computer is represented in binary through the numbers 0 and 1, in theory, there are many ways to represent negative numbers on the computer . We are interested in how to represent the quantity sign and 2's complement. Method of representing the quantity sign: According to the principle of representing the quantity sign, the leftmost bit will represent the sign, an 8-bit byte will have 7 bits (minus the bit). sign) is used to represent numbers from 0000000 (0 10 ) to 1111111 (127 10 ). When using the sign bit, the meaning of the upper 7 bits changes, and we can represent numbers from −127 10 to +127 10 . In the sign method, the number 0 can be represented in two forms, namely 00000000 (+0) and 10000000 (−0).
However, this method is easy to cause confusion, for example: the number 143 if converted to binary, the number will be represented as 10001111, but try this program on c: #include <stdio.h> #include <stdlib.h> void writebitwise(int n){ char buffer [33]; itoa (n,buffer,2); printf ("binary: %sn",buffer); } int main(){ int n = 10; writebitwise(-15); } The number -15 will be represented as a sequence 11111111111111111111111111110001 (10001111), which is easy to confuse, and when doing calculations with binary numbers it is quite confusing because of the sign. We'll go to the 2's complement method for representing negative binary numbers:
- First, the sign bit is 0 if the number is positive, and 1 if the number is negative.
- Second, use the bitwise operator NOT to invert all the bits of a positive binary number (calculate the sign bit) to represent the corresponding negative number.
Example: The number 5 10 represented in binary would be 00000101. The number −5 10 represented in binary (8-bit denominator) is 11111010. To represent 2's complement, add 1 to the number. binary in 1's complement, which adds 1 to 11111010: 11111010 + 1 = 11111011. So 11111011 is the 2's complement representation of −5 10 in a computer.
