Handling outliers.

24-07-2022
chuong xuan
0 Comments

Outliers or outliers are data points that are different from the dateset overview. Suppose the age value is negative or a country is not listed on the map. We can completely use some functions in python to determine the outliers.

Example of outliers : Suppose a class has 100 students out of which 99 get 4 points and the other one gets 10 points. In another class everyone in the class got 6 points. Thus, if you want to evaluate which class is better, you need to determine the average of each student in each class. Obviously, if the total score is calculated, class A has a higher score, but in reality, class B is better.

Mục lục

Aliens in machine learning

When the data has outliers, it will definitely affect the quality of the model. Take a look at the example below:

There is a standard dataset containing the height and weight of each person and a dataset containing some outliers.

import pandas as pd
df_example = pd.DataFrame(
    data={
        "height": [147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "weight": [49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
        "height_2": [110, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "weight_2": [49, 90, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
  } ) df_example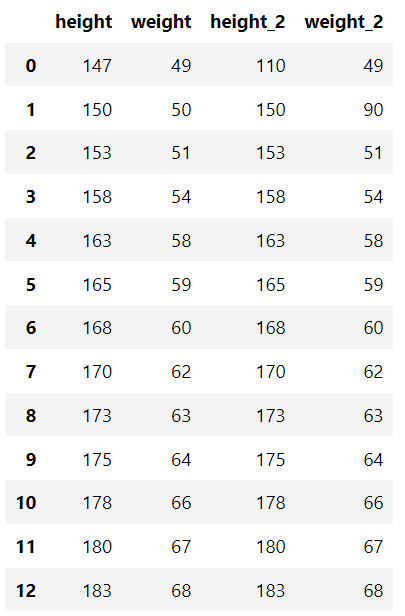

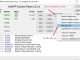
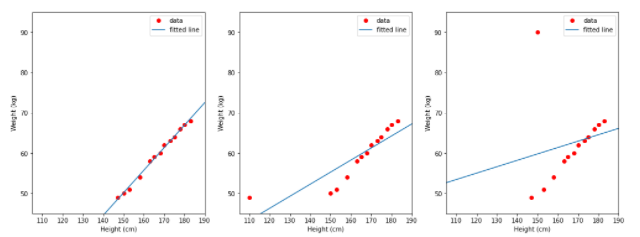
Looking at the data above, it can be seen that height and weight are directly proportional, meaning that the taller a guy is, the heavier he will be. Perhaps the linear regression model will fit this data. Let's consider 3 cases to determine the results of the linear model.

TH1 (left): use the data in the height column as input, in the weight column as the label.
TH2 (middle): uses the data in the height_2 column as input, in the weight column as the label.
TH3 (right): use the data in the height column as input, in the weight_2 column as the label.

 from matplotlib import pyplot as plt from sklearn.linear_model import LinearRegression
def fit_linear_regression_and_visualize( df: pd.DataFrame, input_col: str, label_col: str ): # fit the model by Linear Regression lin_reg = LinearRegression(fit_intercept= True ) lin_reg.fit(df[[input_col]], df[label_col]) w1 = lin_reg.coef_ w0 = lin_reg.intercept_ # visualize plt.plot(df[input_col], df[label_col], "ro", label="data") plt.axis([105, 190, 45, 75]) plt.xlabel("Height (cm)") plt.ylabel("Weight (kg)") plt.ylim(45, 95) plt.plot([105, 190], [w1 * 105 + w0, w1 * 190 + w0], label="fitted line") plt.legend() plt.figure(figsize=(17, 6)) plt.subplot(1, 3, 1) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight") plt.subplot(1, 3, 2) fit_linear_regression_and_visualize(df_example, input_col="height_2", label_col="weight") plt.subplot(1, 3, 3) fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight_2")

The blue line is the line that the model learned. Looking at the 3 images above, we can see that the figure on the left of the line is quite consistent with the data. Thus, there is a simple comment that whether outlier data in the input of the model or the output label affects the correctness of the model.

How to identify and handle outliers that are numbers.

There are 2 main types of outliers:

The values are not in the specified range of the data. For example, age, score or distance cannot be negative.
The value is likely to happen but the probability is very low. For example, a student who takes the test 100 times gets 1 point, but 1 time gets 10 points. These values are likely to occur but are really rare.

How to handle :

With data in the first group, we can replace it with nan and consider that value to be missing and proceed to process it in the missing data processing step.
For data in the second group, usually the upper or lower bound method (clipping or capping) is used. That is, a value that is too large or too small, we bring it to the maximum or minimum value, which is considered a point that is not in the outlier. For example, if there is a city in longitude and latitude outside the limits of the map, we can consider it in terms of latitude and longitude closest to it and no exception. (You can use python to determine the exception range.)

IQR method.

To illustrate how to use the box plot, we will use the California Housing dataset.

import pandas as pd housing_path ="https://media.githubusercontent.com/media/tiepvupsu/tabml_data/master/california_housing/" df_housing = pd.read_csv(housing_path + "housing.csv") df_housing.head()

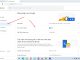
Below is the histogram and box plot of the total_rooms column

import matplotlib.pyplot as plt fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5)) df_housing[["total_rooms"]].hist(bins=50, ax=axes[0]); df_housing[["total_rooms"]].boxplot(ax=axes[1], vert= False );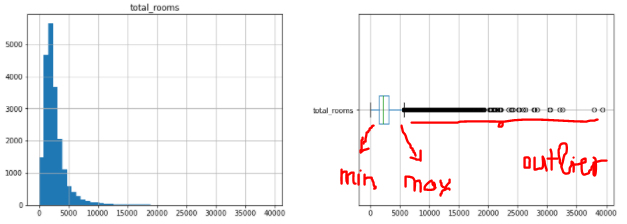

We see in the figure that there are quite a few sporadic values towards the right. So we need to bring them to the minimum or maximum value of Boxplot. Here I use sklearn API to do this.

from typing import Tuple from sklearn.base import BaseEstimator, TransformerMixin def find_boxplot_boundaries( col: pd.Series, whisker_coeff: float = 1.5 ) -> Tuple[float, float]: """Findx minimum and maximum in boxplot. Args: col: a pandas serires of input. whisker_coeff: whisker coefficient in box plot """ Q1 = col.quantile(0.25) Q3 = col.quantile(0.75) IQR = Q3 - Q1 lower = Q1 - whisker_coeff * IQR upper = Q3 + whisker_coeff * IQR return lower, upper class BoxplotOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, whisker_coeff: float = 1.5): self.whisker = whisker_coeff self.lower = None self.upper = None def fit(self, X: pd.Series): self.lower, self.upper = find_boxplot_boundaries(X, self.whisker) return self def transform(self, X): return X.clip(self.lower, self.upper)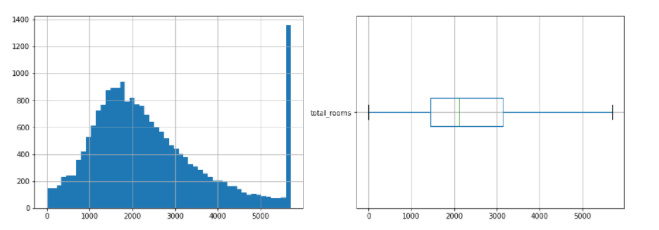

A little explanation of what IQR-Inter Quartile Range means using the middle quartile range, Determined by which values outside the range -1.5xIQR to 1.5xIQR are considered outliers.

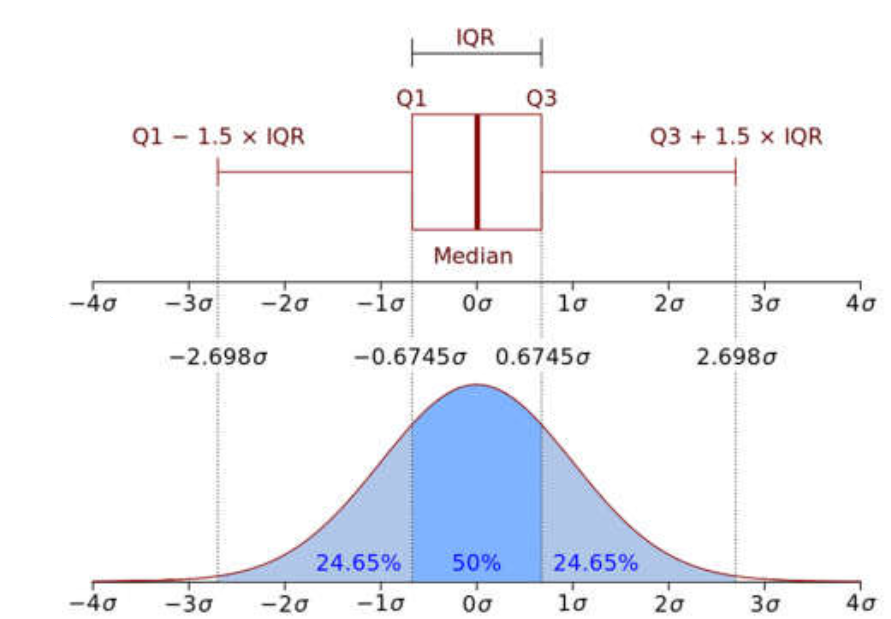
(Q1–1.5 IQR) represents the minimum value of the data set.
(Q3+1.5 IQR) Represents the maximum value of the data set.

After slicing the data according to the maximum and minimum of the boxplot, we see that the data has been less skewed. And we no longer see outliers outside the maximum and minimum.

The Z score method .

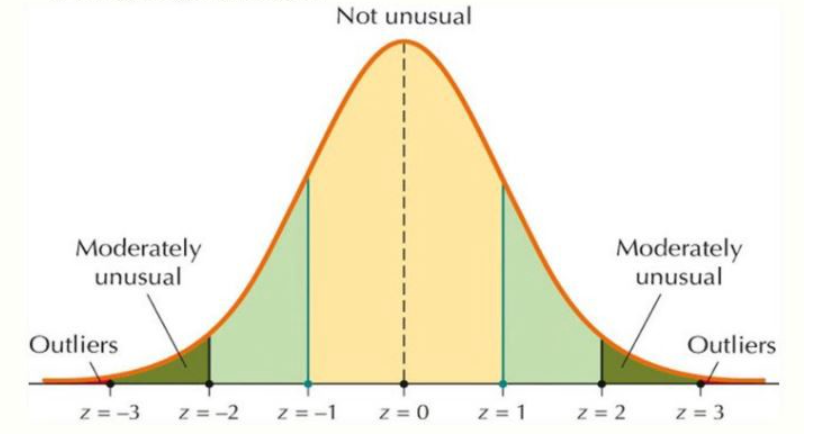
If the data follows a normal distribution, you can apply the 3σ rule to the normal distribution.

In a normal distribution, let μ be the expectation and σ the standard deviation. The 3σ rule for the normal distribution says that:

68% of data points are within μ±σ
95% of the data points are within μ±2σ
99.7% of data points are within μ±3σ

For a data point, its z score is calculated by:

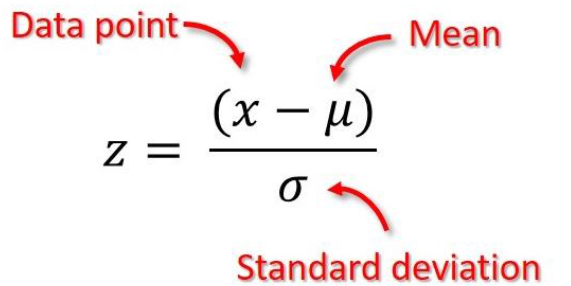
Thus, points with z-score that can be considered outliers are outside the range [-3, 3]. Transforming the math a bit, this is equivalent to having points outside the interval [μ−3σ,μ+3σ] being treated as outliers.

 class ZscoreOutlierClipper (BaseEstimator, TransformerMixin): def __init__(self, z_threshold: float = 3): self.z_threshold = z_threshold self.lower = None self.upper = None def fit(self, X: pd.Series): mean = X.mean() std = X.std() self.lower = mean - self.z_threshold * std self.upper = mean + self.z_threshold * std return self def transform(self, X): return X.clip(self.lower, self.upper)

Try it out with the example above

clipped_total_rooms2 = ZscoreOutlierClipper().fit_transform(df_housing["total_rooms"]) clipped_total_rooms2.hist(bins=50);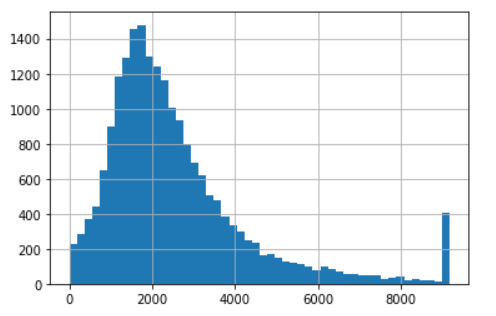

Comment:

Compared to the box plot, z score in this case returns a wider range of values, values greater than 9000 are considered outliers while the upper bound of boxplot is only about 6000.
When the z score exception handling can shift the expectation and standard deviation so the upper and lower bounds will also change. That is, the next determination will be different from the current one.
As for IQR, no matter what the outliers are, it will not affect the upper and lower bounds, because it only needs to replace the outliers into the upper or lower bounds.

The way outliers are identified and handled is categorical.

Unlike numeric data, outlier data in categorical fields are more difficult to identify. Part of that is difficult to plot histograms and identifying outliers requires specialized knowledge.

With value exception can occur in one of the following cases:
Due to the difference in input method. For example, the names of cities, so we need to return them to a normalized form to easily eliminate outliers.
Or it could be a typo, for processing we can plot a histogram showing the frequency of each value in the entire data. Usually the spelling errors will be low.
For some data related to the label data that has many different data that are difficult to one-hot or enlable, we can group them into new items that have something in common. For example: Name of house number, then we can determine whether that house is in a corner, in an alley or on a big street from which to determine the house price.