Biểu diễn số nguyên dưới dạng nhị phân và các phép toán hệ nhị phân
Hệ nhị phân (còn được gọi là hệ đếm cơ số 2) là một hệ đếm chỉ dùng hai ký tự là 0 và 1 để biểu đạt một giá trị số, hệ nhị phân này thường được đề cập tới khi học c,c++ , nhập môn lập trình và khoa học máy tính. Bài viết này sẽ giúp các bạn hiểu được cách biểu diễn một số nguyên dưới dạng nhị phân và thực hiện các phép toán dưới dạng nhị phân.
Mục lục
1.Biểu diễn số thập phân dưới dạng nhị phân:
Chúng ta đến với ví dụ một số 31 và 33 khi biểu diễn dưới dạng nhị phân như sau:
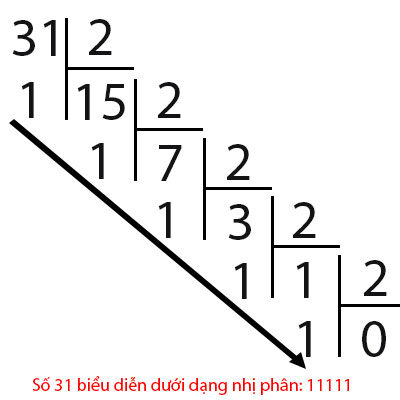
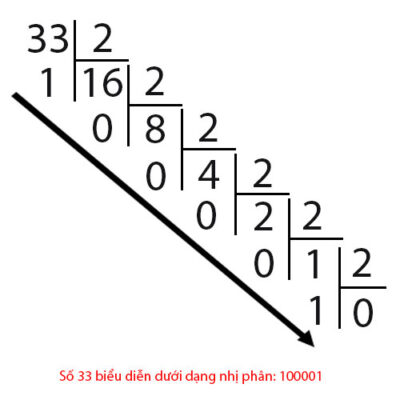
Vậy từ số nhị phân, làm thế nào để biểu diễn ra số thập phân ? Chúng ta hãy nhìn ví dụ theo hình dưới:
2. Biểu diễn số nhị phân dưới dạng số thập phân
Với mỗi đơn vị mang giá trị 1, làm phép tính mũ 2 tăng thêm 1 lần tính từ phải qua, và làm phép tính theo công thức sau:
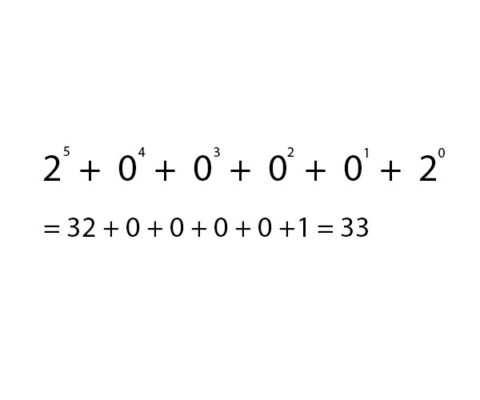
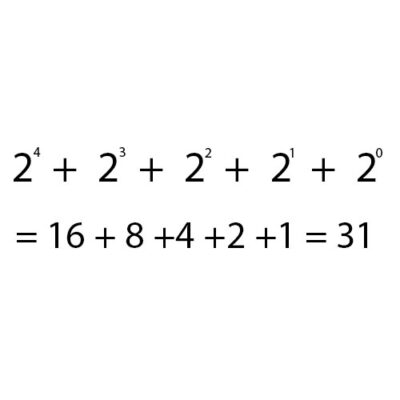
3. Cộng 2 số nhị phân
Để cộng hai số nhị phân, chúng ta áp dụng quy tắc:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (nhớ 1)
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (nhớ 1)
Ví dụ: Cộng hai số “1000111” và số “11110”
1 0 0 0 1 1 1 (71)
+ 1 1 1 1 0 (30)
-------------
= 1 1 0 0 1 0 1 (101)4. Trừ 2 số nhị phân
Để trừ 2 số nhị phân, chúng ta áp dụng quy tắc:
0 − 0 = 0
0 − 1 = 1 (mượn 1)
1 − 0 = 1
1 − 1 = 0
0 − 1 = 1 (mượn 1)
1 − 0 = 1
1 − 1 = 0
1 1 0 1 1 1 0
− 1 0 1 1 1
---------------
= 1 0 1 0 1 1 1
5. Biểu diễn số âm dưới dạng nhị phân
Trước khi vào khái niệm bạn, có thể đọc qua link này để tham khảo: https://vi.wikipedia.org/wiki/Bi%E1%BB%83u_di%E1%BB%85n_s%E1%BB%91_%C3%A2m
Như chúng ta đã hiểu, mọi ký tự hay các số dương và âm trong máy tính đều biểu diễn dưới dạng nhị phân thông qua các số 0 và 1, theo lý thuyết, có nhiều cách để biểu diễn số âm trên máy tính. Chúng ta quan tâm tới cách biểu diễn dấu lượng và bù 2.
Phương pháp biểu diễn dấu lượng:
Theo nguyên tắc biểu diễn dấu lượng, thì bit cực trái sẽ biểu diễn dấu, một byte 8 bit sẽ có 7 bit (trừ đi bit dấu) được dùng để biểu diễn cho các số có giá trị từ 0000000 (010) đến 1111111 (12710). Khi sử dụng bit dấu, ý nghĩa của 7 bit trên sẽ thay đổi, và ta có thể biểu diễn các số từ −12710 đến +12710. Trong phương pháp dấu lượng, số 0 có thể được biểu diễn ở hai dạng, đó là 00000000 (+0) và 10000000 (−0).
Tuy nhiên phương pháp này dễ gây ra sự nhầm lẫn, ví dụ: số 143 nếu quy đổi ra hệ nhị phân, số sẽ được biểu diễn thành 10001111, nhưng hãy thử với chương trình này trên c:
#include <stdio.h>
#include <stdlib.h>
void writebitwise(int n){
char buffer [33];
itoa (n,buffer,2);
printf ("binary: %s\n",buffer);
}
int main(){
int n = 10;
writebitwise(-15);
}
Số -15 sẽ được biểu diễn thành 1 dãy 11111111111111111111111111110001 (10001111), thật dễ gây nhầm lẫn, và khi làm phép tính với số nhị phân khá rẳc rối vì phải xét dấu.
Chúng ta sẽ đi tới phương pháp bù 2 để biểu diễn số âm nhị phân:
- Thứ nhất, bit dấu 0 nếu số là số dương, và 1 nếu số là số âm.
- Thứ hai, sử dụng toán tử thao tác bit (bitwise) NOT để đảo tất cả các bit của số nhị phân dương (tính bit dấu) để biểu diễn số âm tương ứng.
Ví dụ: Số 510 biểu diễn dưới dạng nhị phân sẽ là 00000101 số −510 được biểu diễn sang hệ nhị phân (xét mẫu 8 bit) là 11111010. Để biểu diễn theo phương pháp bù 2, ta cộng thêm 1 vào số nhị phân ở bù 1, tức cộng 1 cho 11111010: 11111010 + 1 = 11111011. Vậy 11111011 là biểu diễn bằng bù 2 của −510 trong máy tính.
2 Comments