Giới Thiệu

Thuật toán Tìm kiếm Hàm mũ (Exponential Search) là một phương pháp tìm kiếm trong danh sách đã được sắp xếp, kết hợp giữa tìm kiếm nhị phân và tìm kiếm tuần tự. Thuật toán này đặc biệt hiệu quả khi danh sách lớn và mục tiêu nằm gần cuối danh sách. Nó hoạt động bằng cách mở rộng khoảng tìm kiếm theo hàm mũ cho đến khi phạm vi tìm kiếm đủ lớn để bao phủ phần tử mục tiêu hoặc vượt quá danh sách.

Ý Tưởng

Ý tưởng chính của thuật toán Tìm kiếm Hàm mũ bao gồm các bước sau:

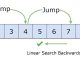
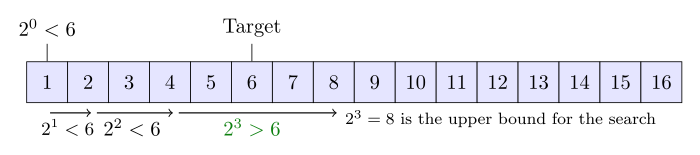
1. Tìm Vị Trí Tìm Kiếm: Bắt đầu từ chỉ số 1 và tiếp tục nhân chỉ số đó với 2 (hoặc 2^k) để mở rộng phạm vi tìm kiếm theo hàm mũ, cho đến khi chỉ số vượt qua hoặc đạt đến phần tử mục tiêu hoặc vượt quá kích thước của danh sách.
2. Sử dụng Tìm kiếm Nhị phân: Khi tìm thấy phạm vi chứa phần tử mục tiêu, thực hiện tìm kiếm nhị phân trong khoảng đó để xác định vị trí chính xác của phần tử mục tiêu.

Ví Dụ

Dưới đây là một ví dụ về thuật toán Tìm kiếm Hàm mũ được triển khai bằng Java:

public class ExponentialSearchExample {
    // Phương thức thực hiện tìm kiếm hàm mũ
    public static int exponentialSearch(int[] arr, int target) {
        int n = arr.length;

        // Bước 1: Kiểm tra phần tử đầu tiên
        if (arr[0] == target) {
            return 0;
        }

        // Bước 2: Tìm phạm vi tìm kiếm
        int i = 1;
        while (i < n && arr[i] <= target) {
            i *= 2; // Mở rộng phạm vi tìm kiếm theo hàm mũ
        }

        // Bước 3: Tìm kiếm nhị phân trong phạm vi tìm kiếm xác định
        return binarySearch(arr, target, i / 2, Math.min(i, n - 1));
    }

    // Phương thức thực hiện tìm kiếm nhị phân
    private static int binarySearch(int[] arr, int target, int left, int right) {
        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (arr[mid] == target) {
                return mid; // Trả về chỉ số của phần tử nếu tìm thấy
            }

            if (arr[mid] < target) {
                left = mid + 1; // Tìm kiếm trong nửa bên phải
            } else {
                right = mid - 1; // Tìm kiếm trong nửa bên trái
            }
        }

        return -1; // Trả về -1 nếu không tìm thấy phần tử mục tiêu
    }

    // Phương thức để in mảng
    public static void printArray(int[] arr) {
        for (int i : arr) {
            System.out.print(i + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] array = {1, 2, 4, 8, 16, 32, 64, 128, 256, 512};
        int target = 64;

        System.out.println("Mảng ban đầu:");
        printArray(array);

        int index = exponentialSearch(array, target);

        if (index != -1) {
            System.out.println("Phần tử " + target + " được tìm thấy tại chỉ số " + index);
        } else {
            System.out.println("Phần tử " + target + " không được tìm thấy trong mảng.");
        }
    }
}

Đánh Giá Thuật Toán Tìm Kiếm Hàm Mũ

Độ phức tạp thuật toán:

• Trường hợp tốt: O(log n) (Khi phần tử mục tiêu nằm gần đầu danh sách và phạm vi tìm kiếm được xác định nhanh chóng)
• Trung bình: O(log n + log n) = O(log n) (Số lần mở rộng phạm vi tìm kiếm và tìm kiếm nhị phân trong khoảng)
• Trường hợp xấu: O(log n + log n) = O(log n) (Khi phần tử mục tiêu nằm gần cuối danh sách hoặc không có trong danh sách)

Không gian bộ nhớ sử dụng: O(1) (Chỉ sử dụng một lượng bộ nhớ cố định)

Tại chỗ (In-place): Có

Cách sử dụng:

Tìm kiếm Hàm mũ có thể được áp dụng trong các tình huống sau:

• Danh sách đã được sắp xếp: Khi danh sách đã được sắp xếp, thuật toán hoạt động hiệu quả.
• Danh sách lớn với phần tử mục tiêu gần cuối: Khi danh sách có kích thước lớn và phần tử mục tiêu nằm gần cuối, tìm kiếm hàm mũ có thể giúp giảm số lượng phần tử cần kiểm tra so với tìm kiếm tuần tự.
• Khi muốn tối ưu hóa tìm kiếm: Khi cần tìm kiếm nhanh chóng trong các danh sách lớn, thuật toán này cung cấp hiệu suất tốt hơn so với tìm kiếm tuần tự.

Tìm kiếm Hàm mũ là một phương pháp tìm kiếm hiệu quả cho các danh sách đã được sắp xếp với kích thước lớn, giúp giảm số lượng phần tử cần kiểm tra so với tìm kiếm tuần tự và kết hợp với tìm kiếm nhị phân để tối ưu hóa quá trình tìm kiếm.