Cấu trúc dữ liệu Mảng (Array)

16-12-2024
Toanngo92
0 Comments

Khái niệm Cấu trúc dữ liệu Mảng

1. Định nghĩa

Mảng (Array) là một cấu trúc dữ liệu lưu trữ một tập hợp các phần tử có cùng kiểu dữ liệu, được tổ chức theo thứ tự và nằm liền kề nhau trong bộ nhớ. Mỗi phần tử của mảng được xác định bởi chỉ số (index).

2. Đặc điểm của mảng

Kích thước cố định: Số lượng phần tử của mảng được xác định tại thời điểm khai báo và không thể thay đổi trong suốt quá trình thực thi chương trình.
Các phần tử có cùng kiểu dữ liệu: Ví dụ, mảng có thể lưu toàn bộ số nguyên, số thực hoặc chuỗi, nhưng không thể lưu lẫn lộn các kiểu dữ liệu.
Lưu trữ liên tiếp trong bộ nhớ: Các phần tử của mảng được sắp xếp liền kề, giúp truy cập nhanh thông qua chỉ số.
Truy cập trực tiếp (Direct Access): Có thể truy cập phần tử bất kỳ bằng chỉ số mà không cần duyệt qua các phần tử khác.

3. Cách hoạt động

Khai báo mảng: Cần xác định kiểu dữ liệu, tên mảng và kích thước của mảng.
- Ví dụ (C/C++): int arr[5]; // Mảng lưu 5 số nguyên
Truy cập phần tử: Sử dụng chỉ số để đọc hoặc ghi giá trị.
- Ví dụ: arr[0] = 10; // Gán giá trị 10 vào phần tử đầu tiên cout << arr[0]; // In giá trị phần tử đầu tiên (10)

4. Ưu điểm

Truy cập nhanh: Nhờ lưu trữ liên tiếp và chỉ số cố định, việc truy cập phần tử diễn ra với thời gian O(1).
Dễ sử dụng: Cấu trúc đơn giản, dễ hiểu.

5. Nhược điểm

Kích thước cố định: Không thể thay đổi số lượng phần tử sau khi khai báo.
Lãng phí bộ nhớ: Nếu khai báo kích thước lớn hơn nhu cầu thực tế, bộ nhớ không được sử dụng hiệu quả.
Khó thêm/xóa phần tử: Việc thêm hoặc xóa phần tử đòi hỏi dịch chuyển các phần tử khác trong mảng.

6. Ứng dụng

Mảng thường được sử dụng để:

Lưu trữ danh sách dữ liệu cố định như điểm số, tên học sinh.
Làm nền tảng cho các cấu trúc dữ liệu phức tạp hơn như danh sách liên kết, hàng đợi, ngăn xếp, bảng băm.

Ví dụ minh họa

Giả sử cần lưu điểm của 5 học sinh:

#include <iostream>
using namespace std;

int main() {
    int scores[5] = {90, 85, 78, 92, 88}; // Mảng lưu 5 điểm số

    // Truy cập và in từng phần tử
    for (int i = 0; i < 5; i++) {
        cout << "Điểm học sinh " << i + 1 << ": " << scores[i] << endl;
    }
    return 0;
}

Kết quả:

Điểm học sinh 1: 90
Điểm học sinh 2: 85
Điểm học sinh 3: 78
Điểm học sinh 4: 92
Điểm học sinh 5: 88

Phân tích tiệm cận các thao tác với mảng

1. Giả thuyết cơ sở

Mảng có kích thước nn.
Các phần tử được đánh số từ 0 đến n-1.
Truy cập và thao tác với mảng dựa trên chỉ số (index).

2. Tìm kiếm phần tử trong mảng

Tìm kiếm tuyến tính (Linear Search):
- Cần duyệt từng phần tử từ đầu đến cuối mảng để kiểm tra điều kiện khớp.
- Thời gian thực thi:
  - Trường hợp tốt nhất: O(1) (phần tử cần tìm nằm ở vị trí đầu tiên).
  - Trường hợp xấu nhất: O(n) (phần tử cần tìm nằm ở vị trí cuối cùng hoặc không tồn tại).
  - Trường hợp trung bình: O(n), vì trung bình phải duyệt qua n/2 phần tử.
Tìm kiếm nhị phân (Binary Search) (áp dụng cho mảng đã sắp xếp):
- Mỗi lần chia đôi mảng, kiểm tra giá trị giữa để quyết định hướng tìm kiếm.
- Thời gian thực thi:
  - Trường hợp tốt nhất: O(1) (phần tử ở giữa ngay từ đầu).
  - Trường hợp xấu nhất: O(log⁡n), do mảng bị chia đôi lặp đi lặp lại.
  - Trường hợp trung bình: O(log⁡n).

Giải thích lý do thuật toán O(log n) khi chia 2 lần:

Khái niệm Logarit

Logarit là một khái niệm toán học dùng để giải quyết các bài toán liên quan đến lũy thừa. Cụ thể, logarit là phép toán ngược của phép nâng lũy thừa.

Định nghĩa

Cho hai số thực a > 0 và b > 0 sao cho a!= 0, logarit cơ số a của b là số thực x sao cho:

a ^ x  = b

Ta có

log(a)b = x

Ví dụ:

log(2) 8 = 3
log(10) 100 = 10

Các loại logarit thông dụng

Logarit thập phân (logarit cơ số 10):
Ký hiệu: log(b) (thường bỏ cơ số nếu là 10).
Ví dụ: log(100) =2.
Logarit tự nhiên (logarit cơ số e):
Ký hiệu: lb(b) với e xấp xỉ = 2.718
Ví dụ: ln(e) = 1

Trong phân tích tiệm cận, chia đôi nhiều lần thường dẫn đến độ phức tạp O(log n) vì số lần thực hiện chia đôi phụ thuộc vào logarit cơ số 2 của kích thước bài toán. Điều này xuất phát từ cách logarit mô tả sự giảm dần theo lũy thừa.

Nếu bắt đầu với kích thước n, số lần chia đôi cần thiết để đạt kích thước 1 là số k sao cho:

Do đó, số bước chia đôi tỷ lệ với log(2)n.

Theo tính chất của logarit, Logarit cơ số khác nhau có thể chuyển đổi lẫn nhau thông qua công thức đổi cơ số:

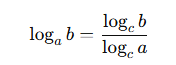
Ví dụ:

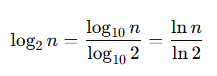
Như vậy, log⁡(2)n, log(⁡10)n, hay ln⁡(n) (logarit tự nhiên) chỉ khác nhau bởi một hằng số nhân.

rong ký hiệu O lớn (Big-O), chúng ta chỉ quan tâm đến tốc độ tăng trưởng (growth rate) của hàm khi nnn tiến tới vô hạn. Các hằng số nhân không ảnh hưởng đến bậc độ phức tạp, vì chúng không làm thay đổi bản chất của hàm khi nnn lớn.

Vì log(2)n, log(10)n, hay ln⁡(n) chỉ khác nhau bởi hằng số, chúng đều thuộc cùng một lớp độ phức tạp O(log n).

3. Thêm phần tử vào mảng

Mảng có kích thước cố định:
- Nếu mảng đã đầy, không thể thêm phần tử.
- Nếu còn chỗ, cần xác định vị trí thêm phần tử:
  - Cuối mảng: Không cần dịch chuyển phần tử, thời gian O(1).
  - Giữa hoặc đầu mảng: Phải dịch chuyển tất cả các phần tử sau vị trí thêm, thời gian O(n)O(n) trong trường hợp xấu nhất.
Mảng có kích thước động (sử dụng cấp phát bộ nhớ động):
- Khi mảng đầy, phải tạo một mảng mới lớn hơn, sao chép dữ liệu cũ sang mảng mới:
  - Thời gian sao chép: O(n).
  - Sau đó, thêm phần tử vào mảng mới: O(1).
  - Tổng thời gian: O(n) khi mảng đầy, O(1) khi chưa đầy.

4. Xóa phần tử khỏi mảng

Mảng có kích thước cố định:
- Sau khi xóa, các phần tử phía sau vị trí xóa phải được dịch chuyển lên để lấp khoảng trống.
- Thời gian thực thi:
  - Trường hợp tốt nhất: O(1) (xóa phần tử cuối, không cần dịch chuyển).
  - Trường hợp xấu nhất: O(n) (xóa phần tử đầu, tất cả các phần tử phải dịch chuyển).
Mảng động:
- Nếu không yêu cầu giữ thứ tự, có thể thay phần tử cần xóa bằng phần tử cuối cùng và giảm kích thước mảng, thời gian O(1).
- Nếu cần giữ thứ tự, phải dịch chuyển phần tử như mảng cố định, thời gian O(n).

5. Tổng kết thời gian tiệm cận

Thao tác	Tốt nhất	Trung bình	Xấu nhất
Tìm kiếm tuyến tính	O(1)	O(n)	O(n)
Tìm kiếm nhị phân	O(1)	O(log⁡n)	O(log⁡n)
Thêm (cuối)	O(1)	O(1)	O(1)
Thêm (giữa hoặc đầu)	O(1)	O(n)	O(n)
Xóa (cuối)	O(1)	O(1)	O(1)
Xóa (giữa hoặc đầu)	O(1)	O(n)	O(n)

6. Nhận xét

Mảng cung cấp thời gian truy cập O(1), nhưng các thao tác thêm và xóa (ở giữa hoặc đầu) có thời gian xấu nhất là O(n).
Tối ưu hoá thao tác thêm/xóa thường cần các cấu trúc khác như danh sách liên kết hoặc vector động (trong C++).

1. Bản chất của truy cập phần tử qua chỉ số

Khi mảng được tạo ra, các phần tử của nó được lưu trữ liên tiếp trong bộ nhớ. Địa chỉ bộ nhớ của phần tử thứ i trong mảng được tính bằng công thức:

i * Base Address + i * (Kích thước phần tử)

Địa chỉ cơ sở: Là địa chỉ của phần tử đầu tiên (A[0]).
Kích thước phần tử: Phụ thuộc vào kiểu dữ liệu (ví dụ: int thường chiếm 4 byte).

Do mảng được lưu trữ liên tiếp, máy tính chỉ cần một phép tính toán học đơn giản để xác định địa chỉ của phần tử và truy xuất giá trị.

2. Thời gian thực thi và tiệm cận

Truy cập phần tử qua chỉ số là một thao tác hằng thời gian.

Thời gian thực thi: O(1) (thời gian không phụ thuộc vào kích thước của mảng nn).

Phân tích toán học:

Máy tính thực hiện các bước:

Lấy địa chỉ cơ sở (A[0]).
Tính địa chỉ phần tử i: i * Base Address + i * (Kích thước phần tử)
Đọc giá trị tại địa chỉ vừa tính.
Tất cả các bước trên đều thực hiện trong thời gian cố định, không phụ thuộc vào n.

3. Tổng kết

Thao tác	Thời gian tốt nhất	Thời gian trung bình	Thời gian xấu nhất
Truy cập phần tử	O(1)	O(1)	O(1)

Lý do thời gian là O(1):
- Mảng lưu trữ liên tiếp, chỉ cần một phép tính toán đơn giản để xác định địa chỉ, không cần duyệt qua bất kỳ phần tử nào khác.
Kết luận: Truy cập phần tử bằng chỉ số trong mảng là một trong những thao tác hiệu quả nhất về mặt thời gian.