Cấu trúc dữ liệu danh sách liên kết (LinkedList)

19-12-2024
Toanngo92
0 Comments

LinkedList là một cấu trúc dữ liệu dạng danh sách liên kết, trong đó các phần tử được liên kết với nhau thông qua các nút (nodes). Mỗi nút chứa hai phần chính:

Dữ liệu (Data): Lưu trữ giá trị thực tế của phần tử.
Con trỏ (Pointer): Trỏ đến nút kế tiếp trong danh sách (hoặc nút trước nếu là danh sách liên kết đôi).

Mục lục

Phân loại LinkedList

Có ba loại danh sách liên kết phổ biến:

Singly Linked List (Danh sách liên kết đơn):

Ví dụ triển khai bằng python

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None  # Trỏ đến nút kế tiếp

class SinglyLinkedList:
    def __init__(self):
        self.head = None  # Điểm bắt đầu của danh sách

    def append(self, data):
        new_node = Node(data)
        if not self.head:  # Nếu danh sách trống
            self.head = new_node
            return
        current = self.head
        while current.next:  # Tìm đến nút cuối
            current = current.next
        current.next = new_node  # Thêm nút mới vào cuối

    def display(self):
        current = self.head
        while current:
            print(current.data, end=" -> ")
            current = current.next
        print("None")

# Sử dụng
sll = SinglyLinkedList()
sll.append(10)
sll.append(20)
sll.append(30)
sll.display()  # Kết quả: 10 -> 20 -> 30 -> None

Doubly Linked List (Danh sách liên kết đôi):

Ví dụ triển khai bằng python

class Node:
    def __init__(self, data):
        self.data = data
        self.prev = None  # Trỏ đến nút trước
        self.next = None  # Trỏ đến nút kế tiếp

class DoublyLinkedList:
    def __init__(self):
        self.head = None  # Điểm bắt đầu của danh sách

    def append(self, data):
        new_node = Node(data)
        if not self.head:  # Nếu danh sách trống
            self.head = new_node
            return
        current = self.head
        while current.next:  # Tìm đến nút cuối
            current = current.next
        current.next = new_node  # Gắn nút mới vào cuối
        new_node.prev = current  # Liên kết ngược về nút trước

    def display(self):
        current = self.head
        while current:
            print(current.data, end=" <-> ")
            current = current.next
        print("None")

# Sử dụng
dll = DoublyLinkedList()
dll.append(10)
dll.append(20)
dll.append(30)
dll.display()  # Kết quả: 10 <-> 20 <-> 30 <-> None

Circular Linked List (Danh sách liên kết vòng):

Ví dụ triển hkai bằng python:

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None  # Trỏ đến nút kế tiếp

class CircularLinkedList:
    def __init__(self):
        self.head = None  # Điểm bắt đầu của danh sách

    def append(self, data):
        new_node = Node(data)
        if not self.head:  # Nếu danh sách trống
            self.head = new_node
            new_node.next = self.head  # Liên kết vòng
            return
        current = self.head
        while current.next != self.head:  # Tìm đến nút cuối
            current = current.next
        current.next = new_node  # Gắn nút mới vào cuối
        new_node.next = self.head  # Liên kết vòng

    def display(self):
        current = self.head
        if not current:
            print("Danh sách rỗng")
            return
        while True:
            print(current.data, end=" -> ")
            current = current.next
            if current == self.head:  # Quay lại nút đầu, dừng lại
                break
        print("(vòng về đầu)")

# Sử dụng
cll = CircularLinkedList()
cll.append(10)
cll.append(20)
cll.append(30)
cll.display()  # Kết quả: 10 -> 20 -> 30 -> (vòng về đầu)

Ưu điểm của LinkedList

Chèn và xoá phần tử nhanh chóng:
- Việc chèn/xoá không cần di chuyển các phần tử khác, chỉ cần thay đổi con trỏ.
Sử dụng bộ nhớ động:
- Không cần cấp phát trước một khối bộ nhớ cố định.
Thích hợp cho cấu trúc dữ liệu phức tạp:
- Dễ dàng triển khai các cấu trúc như hàng đợi (Queue), ngăn xếp (Stack), và đồ thị (Graph).

Nhược điểm của LinkedList

Truy cập tuần tự:
- Không thể truy cập trực tiếp phần tử (như mảng), phải duyệt tuần tự từ đầu danh sách.
Tốn thêm bộ nhớ:
- Mỗi nút cần lưu con trỏ, do đó sử dụng nhiều bộ nhớ hơn mảng.
Khó khăn trong thao tác ngược (với LinkedList đơn):
- Không thể quay lại nút trước khi không có con trỏ trỏ ngược.

Ứng dụng của LinkedList

Triển khai các hàng đợi và ngăn xếp.
Thực hiện undo/redo trong trình soạn thảo văn bản.
Quản lý bộ nhớ động hoặc danh sách công việc (to-do list).
Tạo danh sách liên kết vòng cho các ứng dụng vòng lặp (như lập lịch CPU).

Việc phân tích tiệm cận thao tác với các loại LinkedList (Singly, Doubly, Circular) sẽ dựa vào các phép toán chính như truy cập, tìm kiếm, thêm, và xóa. Tiệm cận tính toán theo độ phức tạp O().

1. Singly Linked List (Danh sách liên kết đơn)

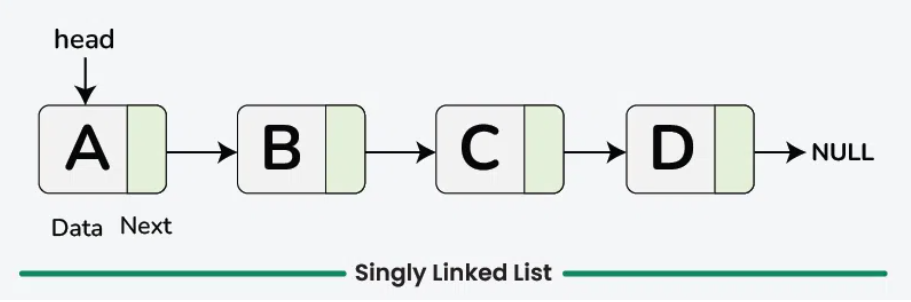
Truy cập

Best/Worst case: O(n)
- Vì phải duyệt tuần tự từ nút đầu đến nút cần truy cập, không có cách truy cập trực tiếp.
- Với nn là số phần tử.

Tìm kiếm

Best case: O(1)
- Nếu phần tử cần tìm nằm ở đầu danh sách.
Worst case: O(n)
- Nếu phần tử nằm ở cuối danh sách hoặc không tồn tại.

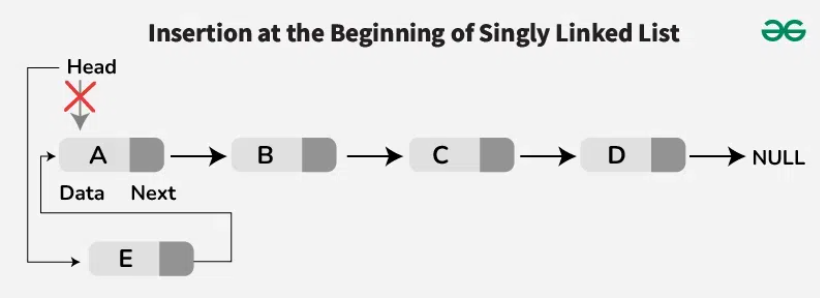
Thêm

Thêm vào đầu: O(1)
- Chỉ cần tạo nút mới và trỏ nó đến nút đầu tiên.
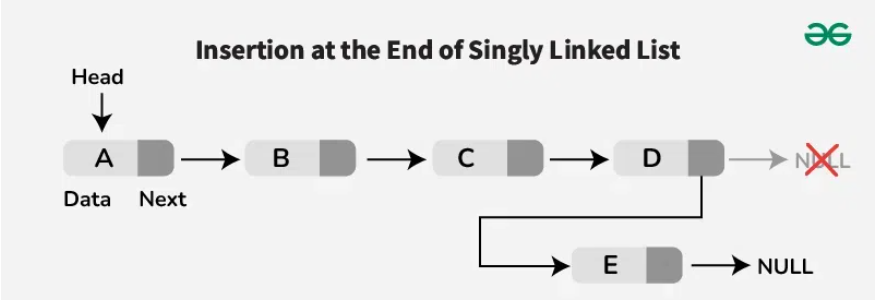
Thêm vào cuối: O(n)
- Phải duyệt đến nút cuối cùng trước khi thêm.

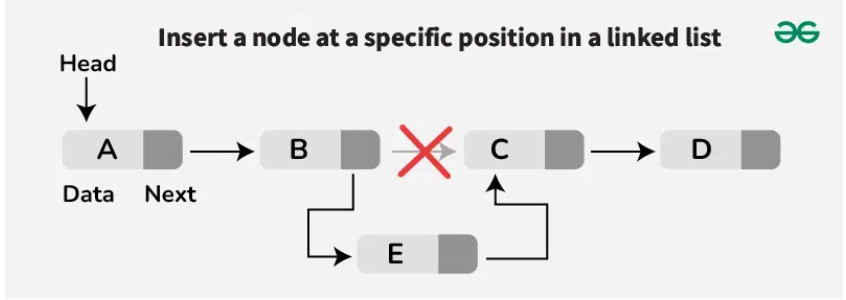
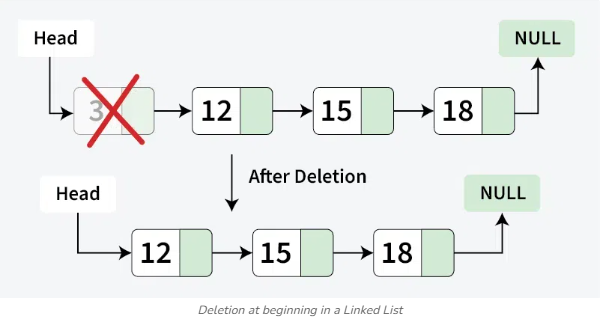
Xóa

Xóa đầu: O(1)
- Chỉ cần thay đổi con trỏ head trỏ đến nút thứ hai.
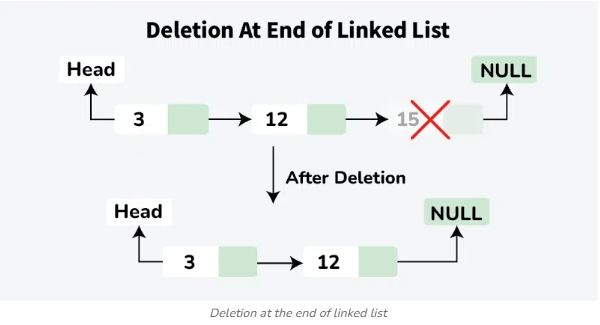
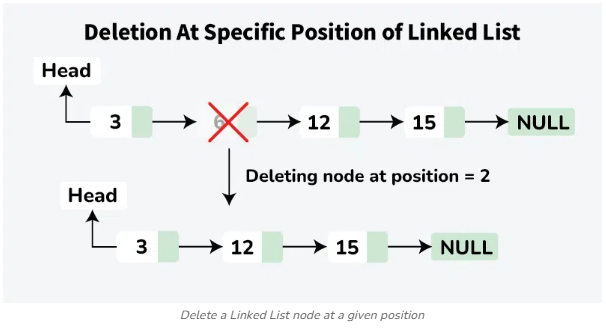
Xóa cuối hoặc giữa: O(n)
- Phải duyệt đến phần tử trước phần tử cần xóa để cập nhật con trỏ.

Tham khảo thêm tại: https://www.geeksforgeeks.org/singly-linked-list-tutorial/

2. Doubly Linked List (Danh sách liên kết đôi)

Truy cập

Best/Worst case: O(n)
- Tương tự LinkedList đơn, cần duyệt tuần tự để truy cập.

Tìm kiếm

Best case: O(1)
- Nếu phần tử nằm ở đầu hoặc cuối (có thể tối ưu nếu lưu trỏ đến cuối).
Worst case: O(n)
- Khi cần duyệt toàn bộ danh sách.

Thêm

Thêm vào đầu/cuối: O(1)
- Dễ dàng vì có trỏ ngược (prev).
Thêm giữa: O(n)
- Phải duyệt tìm vị trí cần thêm.

Xóa

Xóa đầu/cuối: O(1)
- Thao tác đơn giản nhờ trỏ ngược.
Xóa giữa: O(n)
- Phải duyệt đến nút trước nút cần xóa.

3. Circular Linked List (Danh sách liên kết vòng)

Truy cập

Best/Worst case: O(n)
- Duyệt tuần tự như LinkedList đơn, nhưng nếu biết trước cấu trúc thì có thể tiếp tục vòng lặp.

Tìm kiếm

Best case: O(1)
- Nếu phần tử cần tìm là nút đầu.
Worst case: O(n)
- Phải duyệt qua toàn bộ danh sách.

Thêm

Thêm vào đầu/cuối: O(1)
- Đặc biệt nhanh vì có thể tận dụng liên kết vòng, thay đổi trỏ cuối cùng trực tiếp.
Thêm giữa: O(n)
- Tương tự như LinkedList đơn.

Xóa

Xóa đầu/cuối: O(1)
- Dễ dàng vì cấu trúc vòng hỗ trợ.
Xóa giữa: O(n)
- Phải duyệt đến vị trí cần xóa.

Tóm tắt độ phức tạp

Thao tác	Singly Linked List	Doubly Linked List	Circular Linked List
Truy cập	O(n)	O(n)	O(n)
Tìm kiếm	O(n)	O(n)	O(n)
Thêm đầu	O(1)	O(1)	O(1)
Thêm cuối	O(n)	O(1)	O(1)
Xóa đầu	O(1)	O(1)	O(1)
Xóa cuối	O(n)	O(1)	O(1)
Xóa giữa	O(n)	O(n)	O(n)

So sánh thực tế

Singly Linked List:
- Thích hợp khi thao tác chính là thêm/xóa ở đầu danh sách.
- Bộ nhớ tiết kiệm hơn danh sách liên kết đôi.
Doubly Linked List:
- Linh hoạt và dễ thao tác khi cần thêm/xóa ở đầu, cuối hoặc giữa danh sách.
- Tốn thêm bộ nhớ cho con trỏ prev.
Circular Linked List:
- Phù hợp với các ứng dụng cần vòng lặp liên tục như lập lịch CPU hoặc buffer vòng (ring buffer).
- Tối ưu tốc độ thêm/xóa ở đầu/cuối.

Phân tích sự khác biệt giữa danh sách liên kết đôi và danh sách liên kết vòng

1. Khác biệt về cấu trúc

Danh sách liên kết đôi:
- Mỗi nút có hai con trỏ:
  - Một con trỏ trỏ đến nút trước (prev).
  - Một con trỏ trỏ đến nút sau (next).
- Nút đầu (head) có con trỏ prev = None, và nút cuối (tail) có con trỏ next = None.
- Danh sách có điểm đầu và điểm cuối rõ ràng.
Cấu trúc: None <- Node1 <-> Node2 <-> Node3 -> None
Danh sách liên kết vòng:
- Có thể là vòng đơn hoặc vòng đôi:
  - Vòng đơn: Nút cuối trỏ đến nút đầu (chỉ có con trỏ next).Vòng đôi: Nút cuối trỏ đến nút đầu và nút đầu trỏ ngược về nút cuối (cả next và prev).
  Danh sách không có điểm bắt đầu hoặc kết thúc rõ ràng khi duyệt.

2. Khác biệt về cách hoạt động

Điểm bắt đầu và kết thúc

Danh sách liên kết đôi:
- Có điểm đầu (head) và điểm cuối (tail) rõ ràng.
- Khi duyệt đến None, danh sách kết thúc.
- Không tự động quay lại nút đầu.
Danh sách liên kết vòng:
- Không có điểm kết thúc, vì nút cuối trỏ ngược về nút đầu.
- Có thể quay vòng liên tục khi duyệt, nên cần kiểm tra điểm dừng thủ công.

Duyệt danh sách

Danh sách liên kết đôi:
- Duyệt danh sách từ đầu đến cuối hoặc ngược lại từ cuối lên đầu.
- Phù hợp khi cần truy cập hai chiều mà không yêu cầu vòng lặp.
Danh sách liên kết vòng:
- Có thể duyệt tuần hoàn qua danh sách không giới hạn.
- Thích hợp cho các ứng dụng yêu cầu xử lý lặp lại.

Thao tác thêm/xóa

Hiệu suất thêm/xóa ở đầu hoặc cuối tương tự nhau (O(1)O(1)).
Danh sách vòng có lợi thế trong việc thao tác lặp lại nhờ tính vòng lặp tự nhiên.

3. Khác biệt về ứng dụng thực tế

Danh sách liên kết đôi:

Phù hợp cho các ứng dụng không yêu cầu vòng lặp liên tục:
- Trình duyệt: Quản lý lịch sử duyệt web (quay lại và tiến tới).
- Chỉnh sửa văn bản: Undo/redo thao tác.
- Các cấu trúc như Deque: Thêm/xóa ở cả hai đầu.

Danh sách liên kết vòng:

Dùng trong các ứng dụng yêu cầu xử lý vòng lặp liên tục:
- Lập lịch CPU (Round-Robin Scheduling): Xử lý công việc lần lượt theo vòng.
- Hàng đợi vòng (Circular Queue): Phù hợp với hệ thống lưu trữ cố định như bộ nhớ đệm (buffer).
- Game Development: Quản lý vòng đời của các đối tượng hoặc nhân vật.

4. Điểm tương đồng về hiệu suất

Thao tác	Danh sách liên kết đôi	Danh sách liên kết vòng (vòng đôi)
Truy cập	O(n)O(n)	O(n)O(n)
Tìm kiếm	O(n)O(n)	O(n)O(n)
Thêm đầu/cuối	O(1)O(1)	O(1)O(1)
Xóa đầu/cuối	O(1)O(1)	O(1)O(1)

=> Hiệu suất là tương đương, nhưng khác biệt ở cách sử dụng.

Tóm tắt sự khác biệt

Tiêu chí	Danh sách liên kết đôi	Danh sách liên kết vòng
Liên kết cuối	Trỏ đến `None`	Trỏ lại nút đầu, tạo vòng
Kết thúc danh sách	Có điểm đầu và cuối rõ ràng	Không có điểm kết thúc, vòng lặp liên tục
Ứng dụng chính	Undo/redo, deque, trình duyệt lịch sử	Lập lịch CPU, buffer vòng, hàng đợi vòng
Duyệt	Duyệt từ đầu đến cuối hoặc ngược lại	Duyệt vòng lặp liên tục

Khi nào chọn loại nào?

Chọn danh sách liên kết đôi:
- Khi cần truy cập hai chiều nhưng không cần vòng lặp.
- Thích hợp cho các ứng dụng đơn giản, tuyến tính.
Chọn danh sách liên kết vòng:
- Khi ứng dụng cần xử lý liên tục hoặc quay vòng.
- Phù hợp với các thuật toán vòng lặp hoặc tối ưu lưu trữ.