Định lý thợ (Master Theorem)
- 30-09-2024
- Toanngo92
- 0 Comments
Định lý thợ (Master Theorem) là một công cụ mạnh mẽ trong lý thuyết tính toán, dùng để phân tích độ phức tạp thời gian của các giải thuật đệ quy. Nó được sử dụng để giải quyết các phương trình truy hồi dạng chia để trị (Divide and Conquer) phổ biến trong nhiều thuật toán, chẳng hạn như Merge Sort, Quick Sort, và Binary Search.
Mục lục
Mô tả dạng tổng quát của định lý thợ:
Các thuật toán chia để trị thường có dạng phương trình truy hồi như sau:
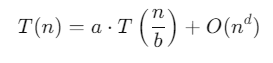
Trong đó:
- n: kích thước của bài toán.
- a: số lượng bài toán con.
- n/b: kích thước của mỗi bài toán con (chia thành b phần).
- T(n/b): thời gian giải mỗi bài toán con.
- O(n^d): chi phí để chia bài toán và kết hợp các kết quả.
Cách áp dụng Định lý thợ:
Có ba trường hợp cần xem xét khi sử dụng Định lý thợ để phân tích độ phức tạp:
Trường hợp 1: Nếu a > b^d
Trong trường hợp này, chi phí giải quyết các bài toán con chiếm ưu thế, do đó:
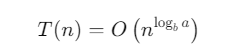
Trường hợp 2: Nếu a = b^d
Trường hợp này, chi phí để chia bài toán và giải quyết bài toán con là cân bằng, dẫn đến:
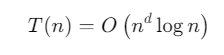
Trường hợp 3: Nếu a < b^d
Trong trường hợp này, chi phí chia và kết hợp chiếm ưu thế, dẫn đến:
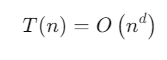
Phân tích chi tiết:
Trường hợp 1: a > b^d
Nếu số lượng bài toán con tăng nhanh hơn so với chi phí chia và kết hợp, chi phí chính là do việc xử lý bài toán con. Trong trường hợp này, chi phí giải bài toán con là lớn nhất.
Ví dụ: Nếu có a = 4, b = 2, d = 1, tức là:
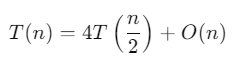
Ở đây, a = 4 và b^d = 2^1 = 2 nên a > b^d.
Theo Định lý thợ, độ phức tạp là:
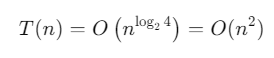
Trường hợp 2: a = b^d
Nếu chi phí xử lý bài toán con và chi phí chia và kết hợp là tương đương, thời gian tổng thể của thuật toán bị chi phối bởi cả hai yếu tố này. Trong trường hợp này, độ phức tạp thời gian là O(n^d log n).
Ví dụ: Nếu a = 2, b = 2, d = 1, tức là:
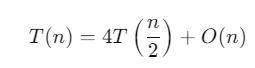
Ở đây, a = 2 và b^d = 2^1 = 2, nên a = b^d.
Theo Định lý thợ, độ phức tạp là:
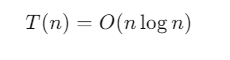
Đây chính là độ phức tạp của thuật toán Merge Sort.
Trường hợp 3: a < b^d
Nếu chi phí chia bài toán và kết hợp các kết quả lớn hơn chi phí xử lý các bài toán con, độ phức tạp thời gian sẽ bị chi phối bởi chi phí chia và kết hợp. Khi đó, độ phức tạp thời gian là O(n^d). Ví dụ: Nếu a = 1, b = 2, d = 1, tức là:
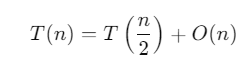
Ở đây, a = 1 và b^d = 2^1 = 2, nên a < b^d.
Theo Định lý thợ, độ phức tạp là:
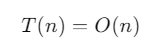
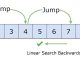
Đây là độ phức tạp của thuật toán tìm kiếm nhị phân (Binary Search).
Định lý thợ giúp chúng ta xác định nhanh chóng độ phức tạp của một giải thuật chia để trị mà không cần phải giải toàn bộ phương trình truy hồi. Nó cung cấp một phương pháp phân tích dựa trên ba trường hợp chính:
- Chi phí giải quyết bài toán con chiếm ưu thế:
T(n) = O(n^{\log_b a}). - Chi phí chia bài toán và kết hợp chiếm ưu thế:
T(n) = O(n^d \log n). - Chi phí chia bài toán và kết hợp thấp hơn:
T(n) = O(n^d).
Bằng cách áp dụng Định lý thợ, ta có thể dễ dàng phân tích các thuật toán chia để trị và hiểu rõ hơn về độ phức tạp thời gian của chúng.