Giải thuật chia để trị (Divide and Conquer) là một trong những phương pháp quan trọng và phổ biến để giải quyết các bài toán phức tạp. Phương pháp này hoạt động bằng cách chia nhỏ bài toán thành các bài toán con có kích thước nhỏ hơn, giải quyết từng bài toán con một cách độc lập, và sau đó kết hợp các kết quả để thu được lời giải của bài toán ban đầu.

Ý tưởng cơ bản của phương pháp chia để trị:

Giải thuật chia để trị gồm ba bước chính:

1. Chia (Divide): Chia bài toán lớn thành các bài toán con nhỏ hơn, thường là chia bài toán thành hai hay nhiều phần có kích thước tương đương nhau.
2. Trị (Conquer): Giải quyết các bài toán con bằng cách sử dụng đệ quy. Nếu bài toán con đủ nhỏ (trường hợp cơ sở – base case), giải trực tiếp không cần chia tiếp.
3. Kết hợp (Combine): Sau khi các bài toán con đã được giải quyết, kết hợp các lời giải để thu được lời giải của bài toán ban đầu.

Ví dụ về giải thuật chia để trị:

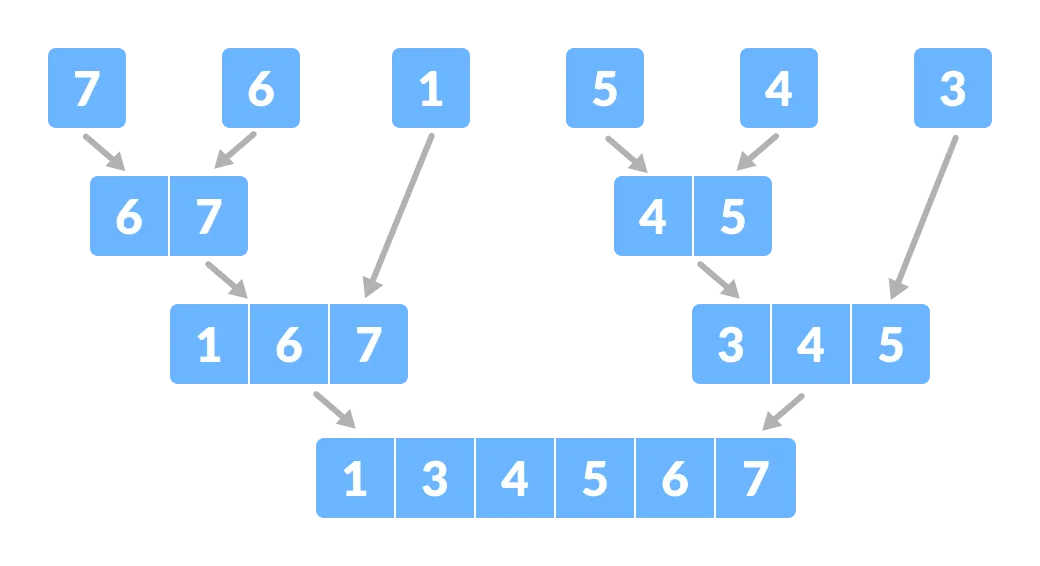
1. Merge Sort (Sắp xếp trộn)

Merge Sort là một thuật toán sắp xếp sử dụng chiến lược chia để trị để sắp xếp một mảng bằng cách chia mảng thành hai nửa, sắp xếp từng nửa và sau đó hợp nhất chúng lại.

Ví dụ cài đặt Merge Sort bằng Java:

public class MergeSort {

    // Hàm chia mảng và thực hiện đệ quy
    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2;

            // Gọi đệ quy chia mảng làm hai nửa
            mergeSort(arr, left, mid);
            mergeSort(arr, mid + 1, right);

            // Gộp hai mảng con đã sắp xếp
            merge(arr, left, mid, right);
        }
    }

    // Hàm gộp hai mảng con
    public static void merge(int[] arr, int left, int mid, int right) {
        int n1 = mid - left + 1;
        int n2 = right - mid;

        int[] L = new int[n1];
        int[] R = new int[n2];

        for (int i = 0; i < n1; ++i)
            L[i] = arr[left + i];
        for (int j = 0; j < n2; ++j)
            R[j] = arr[mid + 1 + j];

        int i = 0, j = 0;
        int k = left;

        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }

        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }

        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }

    public static void main(String[] args) {
        int[] arr = {12, 11, 13, 5, 6, 7};
        mergeSort(arr, 0, arr.length - 1);

        System.out.println("Sorted array: ");
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }
}

Giải thích:

• Chia (Divide): Mảng được chia thành hai phần bằng nhau bằng cách tìm chỉ số giữa (midpoint).
• Trị (Conquer): Sau đó, mỗi nửa mảng được sắp xếp bằng cách gọi đệ quy hàm mergeSort cho đến khi mảng chỉ còn một phần tử (trường hợp cơ sở).
• Kết hợp (Combine): Cuối cùng, các mảng con đã sắp xếp được hợp nhất lại bằng cách sử dụng hàm merge.

Độ phức tạp thời gian của Merge Sort:

• Merge Sort có độ phức tạp thời gian là O(n log n), đây là một thuật toán sắp xếp hiệu quả hơn so với các thuật toán như bubble sort hay insertion sort (có độ phức tạp O(n²)).

2. Tìm kiếm nhị phân (Binary Search)

Tìm kiếm nhị phân là một ví dụ điển hình của giải thuật chia để trị để tìm kiếm một phần tử trong một mảng đã được sắp xếp.

Ví dụ cài đặt Binary Search bằng Java:

public class BinarySearch {

    // Hàm tìm kiếm nhị phân sử dụng đệ quy
    public static int binarySearch(int[] arr, int left, int right, int x) {
        if (right >= left) {
            int mid = left + (right - left) / 2;

            // Nếu phần tử nằm ở giữa
            if (arr[mid] == x)
                return mid;

            // Nếu phần tử nhỏ hơn giá trị ở giữa, tìm ở nửa trái
            if (arr[mid] > x)
                return binarySearch(arr, left, mid - 1, x);

            // Ngược lại, tìm ở nửa phải
            return binarySearch(arr, mid + 1, right, x);
        }

        // Nếu không tìm thấy
        return -1;
    }

    public static void main(String[] args) {
        int[] arr = {2, 3, 4, 10, 40};
        int x = 10;
        int result = binarySearch(arr, 0, arr.length - 1, x);

        if (result == -1)
            System.out.println("Element not present");
        else
            System.out.println("Element found at index " + result);
    }
}

Giải thích:

• Chia (Divide): Mảng được chia thành hai phần bằng cách tìm chỉ số giữa.
• Trị (Conquer): Nếu giá trị cần tìm nhỏ hơn giá trị giữa, chỉ cần tìm trong nửa bên trái, nếu lớn hơn thì tìm trong nửa bên phải.
• Kết hợp (Combine): Trả về chỉ số của phần tử được tìm thấy hoặc báo không tìm thấy.

Độ phức tạp thời gian của Binary Search:

• Độ phức tạp thời gian của thuật toán này là O(log n), rất nhanh đối với các mảng lớn đã được sắp xếp.

Các bài toán ứng dụng giải thuật chia để trị:

• Sắp xếp: Merge Sort, Quick Sort.
• Tìm kiếm: Binary Search.
• Bài toán giải quyết ma trận: Ma trận Strassen để nhân ma trận.
• Tìm số lớn nhất và nhỏ nhất: Tìm giá trị lớn nhất/nhỏ nhất trong một dãy số bằng cách chia mảng thành các phần nhỏ hơn và tìm giá trị trong mỗi phần.

Lợi ích của giải thuật chia để trị:

1. Hiệu suất cao: Trong nhiều trường hợp, giải thuật chia để trị có độ phức tạp thấp hơn các giải thuật khác, ví dụ như Merge Sort có độ phức tạp O(n log n) so với O(n²) của Bubble Sort.
2. Dễ cài đặt với đệ quy: Phương pháp chia để trị thường rất dễ cài đặt với đệ quy vì chia bài toán lớn thành các bài toán con nhỏ hơn và giải quyết dần dần.
3. Có thể song song hóa: Nhiều giải thuật chia để trị có thể được thực hiện song song, giúp tận dụng tốt tài nguyên trên các hệ thống đa nhân (multicore).

Chia để trị là một kỹ thuật rất mạnh mẽ trong lập trình, giúp giải quyết các bài toán phức tạp bằng cách chia nhỏ thành các bài toán đơn giản hơn. Việc áp dụng đúng giải thuật này có thể giúp tăng hiệu quả và tối ưu hóa thời gian thực thi của chương trình.