Giới Thiệu

Thuật toán Tìm kiếm Nhảy (Jump Search) là một phương pháp tìm kiếm được sử dụng để tìm phần tử trong một danh sách đã được sắp xếp. Thuật toán này hoạt động bằng cách “nhảy” qua các phần tử của danh sách với một bước nhảy cố định để giảm số lượng các phần tử cần kiểm tra. Nếu phần tử mục tiêu nằm trong một khoảng giữa các bước nhảy, thuật toán sẽ thực hiện tìm kiếm tuần tự trong khoảng đó. Tìm kiếm Nhảy thường được sử dụng khi danh sách đã được sắp xếp và có kích thước lớn.

Ý Tưởng

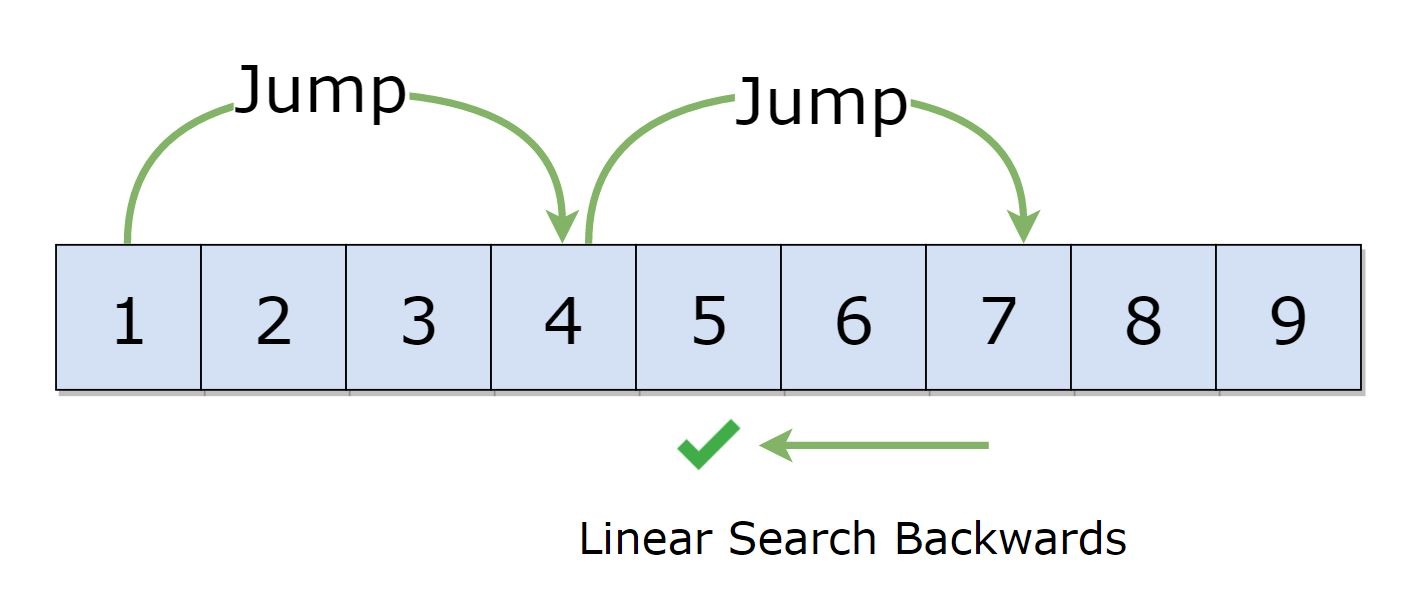
Ý tưởng chính của thuật toán Tìm kiếm Nhảy bao gồm các bước sau:

1. Chọn Bước Nhảy: Định nghĩa kích thước bước nhảy, thường là căn bậc hai của số lượng phần tử trong danh sách (khoảng √n). Điều này giúp cân bằng giữa số lượng bước nhảy và tìm kiếm tuần tự trong mỗi khoảng.
2. Nhảy Qua Các Phần Tử: Duyệt danh sách bằng cách nhảy qua các bước nhảy cho đến khi phần tử mục tiêu nằm trong khoảng giữa hai bước nhảy.
3. Tìm Kiếm Tuần Tự: Khi tìm thấy khoảng chứa phần tử mục tiêu, thực hiện tìm kiếm tuần tự trong khoảng đó để xác định chính xác vị trí của phần tử mục tiêu.

Ví Dụ

Dưới đây là một ví dụ về thuật toán Tìm kiếm Nhảy được triển khai bằng Java:

public class JumpSearchExample {
    // Phương thức thực hiện tìm kiếm nhảy
    public static int jumpSearch(int[] arr, int target) {
        int n = arr.length;
        int step = (int) Math.sqrt(n); // Chọn kích thước bước nhảy
        int prev = 0;

        // Nhảy qua các phần tử
        while (arr[Math.min(step, n) - 1] < target) {
            prev = step;
            step += (int) Math.sqrt(n);
            if (prev >= n) {
                return -1; // Nếu bước nhảy vượt quá kích thước mảng
            }
        }

        // Tìm kiếm tuần tự trong khoảng
        for (int i = prev; i < Math.min(step, n); i++) {
            if (arr[i] == target) {
                return i; // Trả về chỉ số của phần tử nếu tìm thấy
            }
        }

        return -1; // Trả về -1 nếu không tìm thấy phần tử mục tiêu
    }

    // Phương thức để in mảng
    public static void printArray(int[] arr) {
        for (int i : arr) {
            System.out.print(i + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] array = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
        int target = 15;

        System.out.println("Mảng ban đầu:");
        printArray(array);

        int index = jumpSearch(array, target);

        if (index != -1) {
            System.out.println("Phần tử " + target + " được tìm thấy tại chỉ số " + index);
        } else {
            System.out.println("Phần tử " + target + " không được tìm thấy trong mảng.");
        }
    }
}

Đánh Giá Thuật Toán Tìm Kiếm Nhảy

Độ phức tạp thuật toán:

• Trường hợp tốt: O(√n) (Khi phần tử mục tiêu nằm trong khoảng gần phần tử đầu tiên của bước nhảy)
• Trung bình: O(√n + m) (Với m là số phần tử cần kiểm tra trong khoảng tìm kiếm tuần tự)
• Trường hợp xấu: O(√n + m) (Khi phần tử mục tiêu nằm gần cuối hoặc không có trong danh sách)

Không gian bộ nhớ sử dụng: O(1) (Chỉ sử dụng một lượng bộ nhớ cố định)

Tại chỗ (In-place): Có

Cách sử dụng:

Tìm kiếm Nhảy có thể được áp dụng trong các tình huống sau:

• Danh sách đã được sắp xếp: Khi danh sách đã được sắp xếp, thuật toán này hoạt động hiệu quả.
• Kích thước danh sách lớn: Khi danh sách có kích thước lớn, thuật toán giúp giảm số lượng phần tử cần kiểm tra so với tìm kiếm tuần tự.
• Khi bước nhảy có thể xác định hợp lý: Khi bước nhảy có thể được lựa chọn sao cho tối ưu hóa hiệu suất tìm kiếm.

Tìm kiếm Nhảy là một phương pháp tìm kiếm hiệu quả cho các danh sách đã được sắp xếp với kích thước lớn, giúp giảm số lượng phần tử cần kiểm tra so với tìm kiếm tuần tự. Tuy nhiên, tìm kiếm Nhảy không phải lúc nào cũng nhanh hơn so với tìm kiếm nhị phân và cần lựa chọn kích thước bước nhảy hợp lý để đạt hiệu suất tốt nhất.