Giới Thiệu

Thuật toán Tìm kiếm Nhị phân (Binary Search) là một phương pháp tìm kiếm hiệu quả được sử dụng để tìm phần tử trong một danh sách đã được sắp xếp. Thuật toán này hoạt động bằng cách chia danh sách thành hai nửa và so sánh phần tử mục tiêu với phần tử ở giữa danh sách, từ đó quyết định tiếp tục tìm kiếm trong nửa bên trái hoặc bên phải. Tìm kiếm nhị phân là một thuật toán rất phổ biến trong lập trình nhờ vào hiệu suất cao và tính đơn giản khi làm việc với các danh sách lớn.

Ý Tưởng

Thuật toán Tìm kiếm Nhị phân hoạt động theo nguyên tắc chia để trị. Ý tưởng chính là:

1. Chọn phần tử giữa của danh sách (pivot).
2. So sánh phần tử mục tiêu với phần tử giữa:

• Nếu phần tử mục tiêu bằng phần tử giữa, thuật toán trả về chỉ số của nó.
• Nếu phần tử mục tiêu nhỏ hơn phần tử giữa, tiếp tục tìm kiếm trong nửa bên trái của danh sách.
• Nếu phần tử mục tiêu lớn hơn phần tử giữa, tiếp tục tìm kiếm trong nửa bên phải của danh sách.

1. Lặp lại quá trình này cho đến khi tìm thấy phần tử mục tiêu hoặc danh sách không còn phần tử nào để kiểm tra.

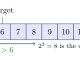
Ví Dụ

Dưới đây là một ví dụ về thuật toán Tìm kiếm Nhị phân được triển khai bằng Java:

public class BinarySearchExample {
    // Phương thức thực hiện tìm kiếm nhị phân
    public static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            // So sánh phần tử mục tiêu với phần tử giữa
            if (arr[mid] == target) {
                return mid; // Trả về chỉ số của phần tử nếu tìm thấy
            }

            if (arr[mid] < target) {
                left = mid + 1; // Tìm kiếm trong nửa bên phải
            } else {
                right = mid - 1; // Tìm kiếm trong nửa bên trái
            }
        }

        return -1; // Trả về -1 nếu không tìm thấy phần tử mục tiêu
    }

    // Phương thức để in mảng
    public static void printArray(int[] arr) {
        for (int i : arr) {
            System.out.print(i + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] array = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
        int target = 7;

        System.out.println("Mảng ban đầu:");
        printArray(array);

        int index = binarySearch(array, target);

        if (index != -1) {
            System.out.println("Phần tử " + target + " được tìm thấy tại chỉ số " + index);
        } else {
            System.out.println("Phần tử " + target + " không được tìm thấy trong mảng.");
        }
    }
}

Đánh Giá Thuật Toán Tìm Kiếm Nhị Phân

Độ phức tạp thuật toán:

• Trường hợp tốt: O(1) (Khi phần tử mục tiêu nằm ở vị trí giữa của danh sách)
• Trung bình: O(log n) (Khi tìm kiếm yêu cầu phân chia danh sách nhiều lần)
• Trường hợp xấu: O(log n) (Khi phần tử mục tiêu không có trong danh sách và phải thực hiện toàn bộ quá trình phân chia)

Không gian bộ nhớ sử dụng: O(1) (Tìm kiếm nhị phân không yêu cầu bộ nhớ phụ lớn, chỉ sử dụng một số biến để theo dõi chỉ số)

Tại chỗ (In-place): Có

Cách sử dụng:

Tìm kiếm nhị phân thường được áp dụng trong các tình huống sau:

• Danh sách đã được sắp xếp: Khi danh sách đã được sắp xếp, thuật toán Tìm kiếm Nhị phân hoạt động rất hiệu quả.
• Yêu cầu hiệu suất cao: Khi cần tìm kiếm nhanh chóng trong các danh sách lớn, thuật toán này cung cấp hiệu suất tốt hơn so với các thuật toán tìm kiếm tuần tự.
• Khi bộ nhớ hạn chế: Với không gian bộ nhớ nhỏ, tìm kiếm nhị phân là lựa chọn tốt vì nó không yêu cầu bộ nhớ phụ lớn.

Tìm kiếm nhị phân là một thuật toán hiệu quả và mạnh mẽ cho các danh sách đã được sắp xếp, cung cấp khả năng tìm kiếm nhanh chóng với độ phức tạp thấp. Tuy nhiên, nó yêu cầu danh sách phải được sắp xếp trước, nếu không, thuật toán sẽ không hoạt động chính xác.