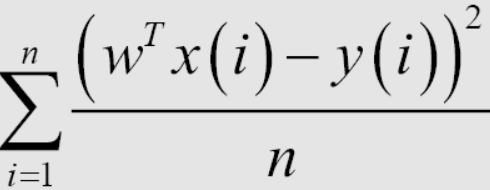
Mô hình Linear regression
- 08-09-2021
- chuong xuan
- 0 Comments
Trong khi chúng ta sử dụng các thư viện có sẵn để training model thì nhưng chúng ta dùng thìa khóa mở một cái hộp mà không biết bên trong nó như thế nào? Nhưng bạn vẫn có thể mở được chiếc hộp. Thì việc hiểu dõ hơn về những lý thuyết bên trong thuật toán giúp bạn có thể sử dụng các tham số sao cho phù hợp với mô hình.
Trong phần này mình sẽ cùng các bạn làm quen với linear regression là một trong những thuật toán cơ bản nhất trong machine learning. Trong thuật toán này thì đâu vào và đầu ra sẽ được mô tả bời một hàm tuyến tính.
Mục lục
Bài toán minh họa
Giả sử có một bài toán dự đoán giá nhà. Có dữ liệu của 1000 căn nhà trong thành phố đó, trong đó ta biết các thông số trong từ ngôi nhà là có chiều rộng là x1 m2 có x2 phòng ngủ và cách trung tâm x3 km. Liệu rằng khi cho thêm một căng nhà mới có các thông số trên bạn có thể dự đoán được giá y của căn nhà? Nếu có thì hàm dự đoán y = f(x) có dạng như thế nào? Ở đây vector đặc trưng x = [x1, x2, x3]T là một vector cột chứa thông tin đầu vào, đầu ra y là một số vô hướng.
Trên thực tế thì ta có thể thấy khi các hệ số của từ features tăng thì đầu ra cũng tăng do vậy có một hàm tuyến tính đơn giản:
y_pre = f(x) = w0 + w1x1 + w2x2 + … + wnxn= xTw
Trong đó:
- y_pre: là giá trị đầu ra dự đoán. (và y_pre sẽ khác y thực tế)
- n là số lượng features.
- (xi) là feature thứ i
- w là tham số của mô hình trong đó w0 là bias và các tham số w1, w2,….
Bài toán trên đây là bài toán dự đoán giá trị của đầu ra dựa trên vector đặc trưng đầu vào. Ngoài ra, giá trị của đầu ra có thể nhận rất nhiều giá trị thực dương khác nhau. Vì vậy, đây là một bài toán regression. Mối quan hệ y_pre = xTw là một mối quan hệ tuyến tính. Tên gọi linear regression xuất phát từ đây.
Huấn luyện mô hình
Sau khi đã có mô hình linear regression, thì việc huấn luyện mô hình là việc tìm ra các tham số tối ưu nhất thông qua bộ dữ liệu huấn luyện. Để làm được điều này chúng ta cần phải có một cách để xác định mô hình có tốt hay không. Sau đây mình sẽ giới thiệu 1 cách để xác định đó là dùng biểu thức Root Mean Square Error(RMSE). Mục tiêu của việc huấn luyện đó là giảm thiểu giá trị của Mean Square Error (MSE). Nó đơn giản là ta muốn sự khác nhau giữa y dự đoán và y thực tế càng nhỏ càng tốt.
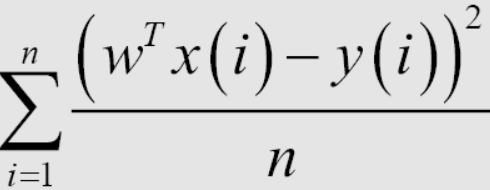
Việc lấy trung bình hệ số 1/n hay tổng trong hàm mất mát, về mặt toán học không ảnh hưởng tới nghiệm của bài toán. Trong machine leanring, các hàm mất mát thường chứa hệ số trung bình theo từng điểm dữ liệu trong tập huấn luyện do vậy khi tính giá trị của hàm mất mát trên tập kiểm thử ta cần tính trung bình lỗi của mỗi điểm. Việc tính hàm mất mát giúp tránh hiện tượng overfitting khi số lượng điểm dữ liệu quá nhiều và nó cũng giúp ta có thể đánh giá được mô hình sau này.
Phương trình chuẩn
Để tìm giá trị w giúp phương trình trên đạt giá trị cực tiểu ta có thể tính đạo hàm của phương trên theo w khi chúng bằng không. Và xác định cực tiểu.
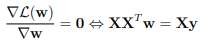
Do vậy ta có thể xác định cực tiểu nhờ công thức sau: w = (XTX)–1XTy.
Trong đó w là gí trị mà MSE(w) đạt cực tiểu. y là vector cần tìm bao gồm (y1, … ym).
Implement bằng python.
Giả sư cho tập dữ liệu bên dưới, hãy xác định cân nặng của người đó dượng theo chiều cao.
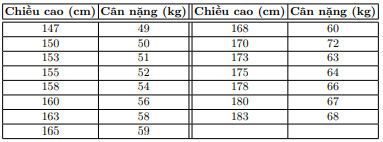
Hiển thị dữ liệu
import numpy as np
import matplotlib.pyplot as plt
X = np.array([[147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183]]).T
y = np.array([ 49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68])
Nhìn vào bài toán ta cần xác định được mô hình có dạng : (cân nặng) = w_1*(chiều cao) + w_0.
Xác định nghiệm theo công thức.
Khởi tạo dữ liệu
one = np.ones((X.shape[0], 1)) #Bias
Xbar = np.concatenate((one, X), axis = 1) # each point is one row
Tiếp theo, chúng ta sẽ tính toán các hệ số w_1 và w_0 dựa vào công thức . Chú ý: giả nghịch đảo của một ma trận A trong Python sẽ được tính bằng numpy.linalg.pinv(A).
A = np.dot(Xbar.T, Xbar)
b = np.dot(Xbar.T, y)
w_best = np.dot(np.linalg.pinv(A), b)
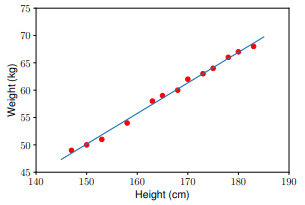
Sử dụng mô hình để dự đoán dữ liệu trong test set:
y1 = w_1 * 155 + w_0
y2 = w_1 * 160 + w_0
print(’Input 155cm, true output 52kg, predicted output %.2fkg’ %(y1) )
print(’Input 160cm, true output 56kg, predicted output %.2fkg’ %(y2))
Kết quả
Input 155cm, true output 52kg, predicted output 52.94kg
Input 160cm, true output 56kg, predicted output 55.74kg
Các bạn cũng có thể thử với một số thư viện của python để so sánh kết quả.
Các bài toán có thể giải được bằng linear regression
Ta thấy công thức XTW là một hàm tuyến tính theo cả w và x. Nhưng trên thực tế linear regression có thể áp dụng cho các mô hình chỉ cần tuyến tính theo w. Ví dụ:
y ≈ w1x1 + w2x2 + w3x21 + w4 sin(x2) + w5x1x2 + w0
Là một hàm tuyến tính theo w và vì vậy cũng có thể được giải bằng linear regression. Tuy nhiên thì việc xác định sin(x2) và x1x2 là tương đối không tự nhiên.
Hạn chế của linear regression
Hạn chế đầu tiên của linear regression là nó rất nhạy cảm với nhiễu (sensitive to noise). Trong ví dụ về mối quan hệ giữa chiều cao và cân nặng bên trên, nếu có chỉ một cặp dữ liệu nhiễu (150 cm, 90kg) thì kết quả sẽ sai khác đi rất nhiều.
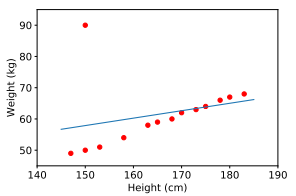
Vì vậy trước khi thực hiện traning model chúng ta cần một bước gọi là tiền xử lý (pre-processing) mình đã nói ở blog trước các bạn có thể tham khảo.
Hạn chế thứ hai của linear regression là nó không biểu diễn được các mô hình phức tạp.
Tổng kết
Vậy là bài này mình đã hướng dẫn các bạn cách huấn luyện thuật toán hồi quy tuyến tính. Chốt lại về cơ bản, để huấn luyện 1 thuật toán cần:
- Định nghĩa được mô hình.
- Định nghĩa hàm chi phí (hoặc hàm mất mát).
- Tối ưu hàm chi phí bằng dữ liệu huấn luyện.
- Tìm ra các trọng số của mô hình mà tại đó hàm chi phí có giá trị nhỏ nhất.