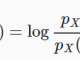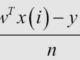
Xử lý các giá trị ngoại lai.

12-09-2021
chuong xuan
0 Comments

Giá trị ngoại lai hay outlier là những điểm dữ liệu khác biệt so với tổng quan của dateset. Giả sử như giá trị tuổi bị âm hay một đất nước không có tên trên bản đồ. Chúng ta hoàn toàn có thể xử dụng một số hàm trong python để xác định các giá trị ngoại lại.

Ví dụ về giá trj ngoại lai: Giả sử một lớp có 100 bạn trong đó 99 bạn được 4 điểm và một bạn còn lại được 10 điểm. Một lớp khác mọi người trong lớp đều được 6 điểm. Như vậy nếu muốn đánh giá xem lớp nào tốt hơn thì cần xác định được bình quân của từng học sinh của mỗi lớp. Dõ ràng nếu tính tổng điểm thì lớp A có số điểm cao hơn nhưng trên thực tế thì lớp B giỏi hơn.

Mục lục

Ngoại lai trong machine learning

Khi dữ liệu có những giữ liệu ngoại lai chắc chắn sẽ làm ảnh hưởng tới chất lượng của mô hình. Cùng xét ví dụ dưới đây:

Có một bộ dữ liệu chuẩn chứa chiều cao và cân nặng của từng người và một dữ liệu chứa một số dữ liệu ngoại lai.

import pandas as pd
df_example = pd.DataFrame(
    data={
        "height": [147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "weight": [49, 50, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
        "height_2": [110, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183],
        "weight_2": [49, 90, 51, 54, 58, 59, 60, 62, 63, 64, 66, 67, 68],
    }
)
df_example

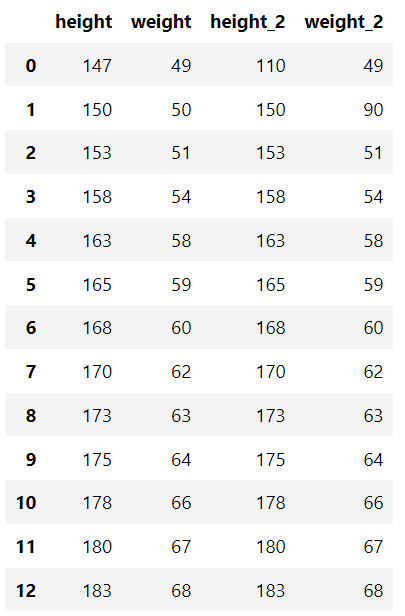
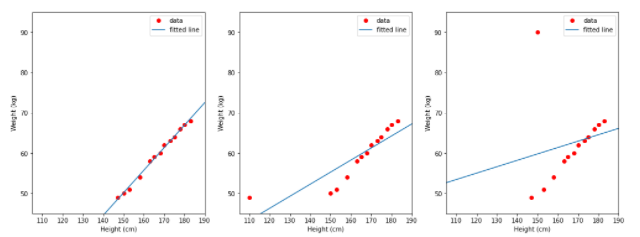
Nhìn vào dữ liệu trên có thể thấy chiều cao và cân nặng tỉ lệ thuận với nhau, nghĩa là nếu thằng nào càng cao thì thằng đó sẽ càng nặng. Có lẽ mô hình hồi quy tuyến tính sẽ phù hợp với dữ liệu này. Cùng xét 3 trường hợp để xác định kết quả của mô hình tuyến tính.

TH1 (trái): dùng dữ liệu trong cột height làm đầu vào, trong cột weight làm nhãn.
TH2 (giữa): dùng dữ liệu trong cột height_2 làm đầu vào, trong cột weight làm nhãn.
TH3 (phải): dùng dữ liệu trong cột height làm đầu vào, trong cột weight_2 làm nhãn.

from matplotlib import pyplot as plt

from sklearn.linear_model import LinearRegression

def fit_linear_regression_and_visualize(
    df: pd.DataFrame, input_col: str, label_col: str
):
    # fit the model by Linear Regression
    lin_reg = LinearRegression(fit_intercept=True)
    lin_reg.fit(df[[input_col]], df[label_col])
    w1 = lin_reg.coef_
    w0 = lin_reg.intercept_

    # visualize
    plt.plot(df[input_col], df[label_col], "ro", label="data")
    plt.axis([105, 190, 45, 75])
    plt.xlabel("Height (cm)")
    plt.ylabel("Weight (kg)")
    plt.ylim(45, 95)
    plt.plot([105, 190], [w1 * 105 + w0, w1 * 190 + w0], label="fitted line")
    plt.legend()

plt.figure(figsize=(17, 6))
plt.subplot(1, 3, 1)
fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight")

plt.subplot(1, 3, 2)
fit_linear_regression_and_visualize(df_example, input_col="height_2", label_col="weight")

plt.subplot(1, 3, 3)
fit_linear_regression_and_visualize(df_example, input_col="height", label_col="weight_2")

Đường màu xanh là đường mà mô hình học được. Nhìn vào 3 hình trên có thể thấy hình bên trái đường thẳng khá khớp so với dữ liệu. Như vậy có nhận xét đơn giản là dù dữ liệu ngoại lệ ở input của mô hình hay nhãn output đều mảng hưởng tới tính đúng của mô hình.

Cách xác định và xử lý các điểm ngoại lai là số.

Có 2 loại ngoại lai chính:

Các giá trị không nằm trong miền xác định của dữ liệu. Ví dụ, tuổi, điểm số hay khoảng cách không thể là số âm.
Giá trị có khả năng xảy ra nhưng xác suất rất thấp. Ví dụ học sinh thi 100 lần được 1 điểm nhưng 1 lần được 10 điểm. Những giá trị này có khả năng xảy ra nhưng thực sự hiếm.

Cách xử lý:

Với dữ liệu thuộc nhóm thứ nhất ta có thể thay bằng nan và coi như giá trị đó bị thiếu và tiến hàng xử lý nó trong bước xử lý missing data.
Với dữ liệu ở nhóm hai, thường thì sẽ sử dụng phương pháp chặn trên hoặc chặn dưới (clipping hay capping). Tức là một giá trị quá lớn hoặc quá nhỏ, ta đưa nó về giá trị lớn nhất hoặc nhỏ nhất, được coi là điểm không thuộc outlier. Ví dụ nếu có một thành phố nào thuộc kinh tuyến và vĩ tuyến ngoài giới hạn của bản đồ ta có thể xét nó về kinh tuyến và vĩ tuyến gần nó nhất và không bị ngoại lệ. ( Có thể xử dụng python để xác định khoảng ngoại lệ).

Phương thức IQR.

Để minh họa cho cách sử dụng box plot, ta sẽ sử dụng bộ dữ liệu California Housing.

import pandas as pd
housing_path ="https://media.githubusercontent.com/media/tiepvupsu/tabml_data/master/california_housing/"
df_housing = pd.read_csv(housing_path + "housing.csv")
df_housing.head()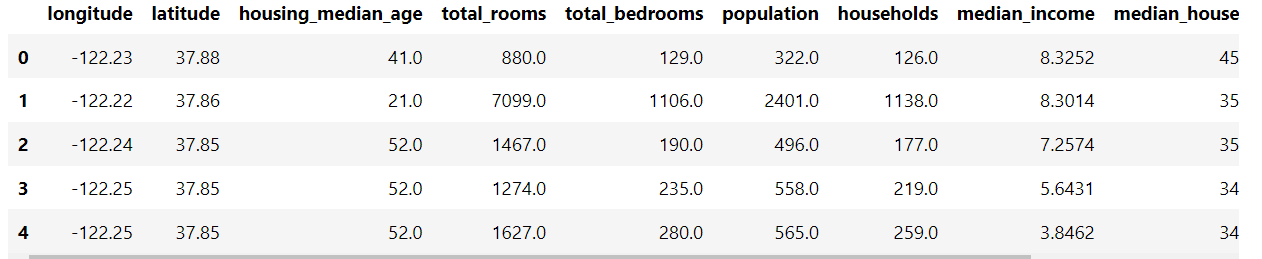

Dưới đây là histogram và box plot của cột total_rooms

import matplotlib.pyplot as plt

fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5))
df_housing[["total_rooms"]].hist(bins=50, ax=axes[0]);
df_housing[["total_rooms"]].boxplot(ax=axes[1], vert=False);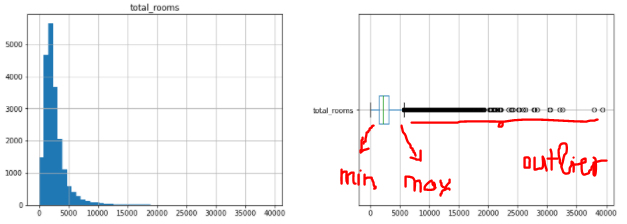

Ta thấy trên hình có khá nhiều giá trị lẻ tẻ hướng về bên phải. Do vậy ta cần đưa chúng về giá trị cực tiểu hoặc cựa đại của Boxplot. Ở đây mình sử dụng sklearn API để làm điều này.

from typing import Tuple
from sklearn.base import BaseEstimator, TransformerMixin


def find_boxplot_boundaries(
    col: pd.Series, whisker_coeff: float = 1.5
) -> Tuple[float, float]:
    """Findx minimum and maximum in boxplot.

    Args:
        col: a pandas serires of input.
        whisker_coeff: whisker coefficient in box plot
    """
    Q1 = col.quantile(0.25)
    Q3 = col.quantile(0.75)
    IQR = Q3 - Q1
    lower = Q1 - whisker_coeff * IQR
    upper = Q3 + whisker_coeff * IQR
    return lower, upper


class BoxplotOutlierClipper(BaseEstimator, TransformerMixin):
    def __init__(self, whisker_coeff: float = 1.5):
        self.whisker = whisker_coeff
        self.lower = None
        self.upper = None

    def fit(self, X: pd.Series):
        self.lower, self.upper = find_boxplot_boundaries(X, self.whisker)
        return self

    def transform(self, X):
        return X.clip(self.lower, self.upper)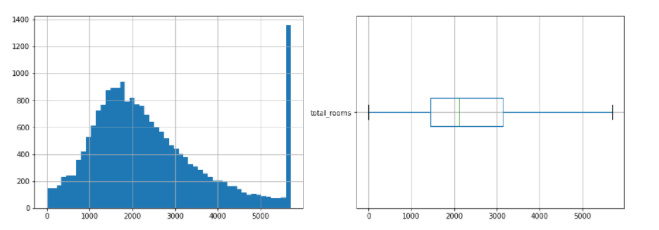

Giải thích một chút về phương thức IQR-Inter Quartile Range có nghĩa là sử dụng dải phần tư giữa, Xác định bằng cách những giá trị nào nằm ngoài phạm vị -1,5xIQR đến 1,5xIQR được coi là giá trị ngoại .

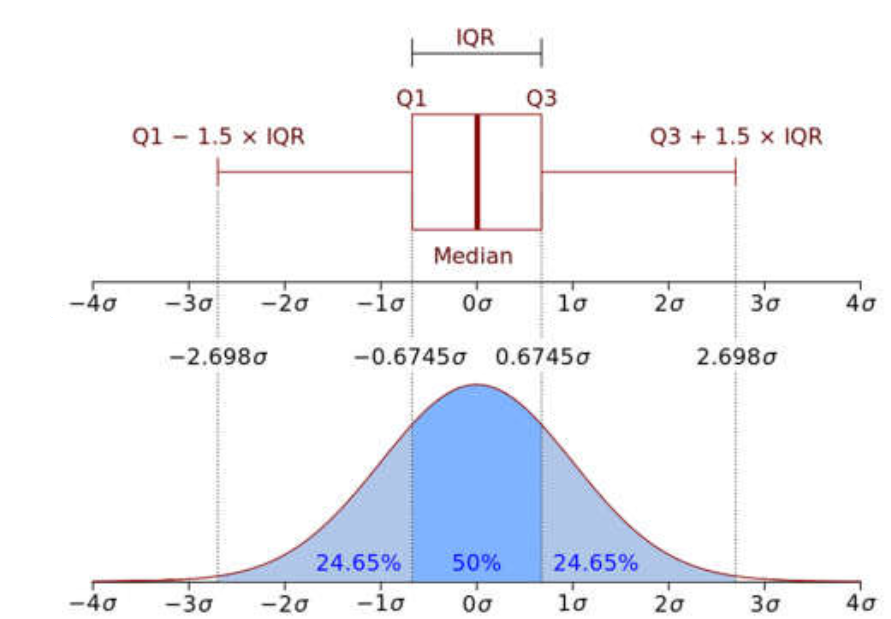
(Q1–1.5IQR) đại diện cho giá trị nhỏ nhất của tập dữ liệu.
(Q3+1.5IQR) Đại diện cho giá trị lớn nhất của tập dữ liệu.

Sau khi cắt dữ liệu theo cực đại và cự tiểu của boxplot ta thấy rằng dữ liệu đã đỡ lệch đi. Và ta không còn thấy các điểm ngoại lai nằm ngoài cực đại và cực tiểu.

Phương thức Z score.

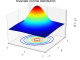
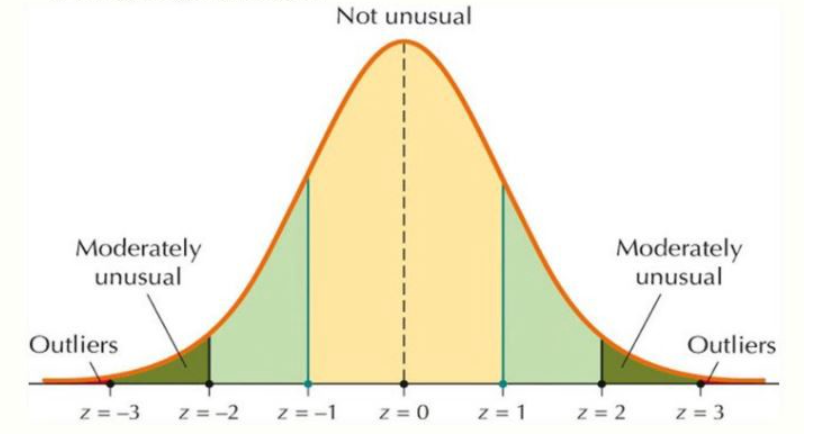
Nếu dữ liệu tuân theo phân phối chuẩn, bạn có thể áp dụng quy tắc 3σ cho phân phối chuẩn.

Trong phân phối chuẩn, giả sử μ là kỳ vọng và σ là độ lệch chuẩn. Quy tắc 3σ cho phân phối chuẩn nói rằng:

68% các điểm dữ liệu nằm trong khoảng μ±σ
95% các điểm dữ liệu nằm trong khoảng μ±2σ
99.7% các điểm dữ liệu nằm trong khoảng μ±3σ

Với một điểm dữ liệu , z score của nó được tính bởi:

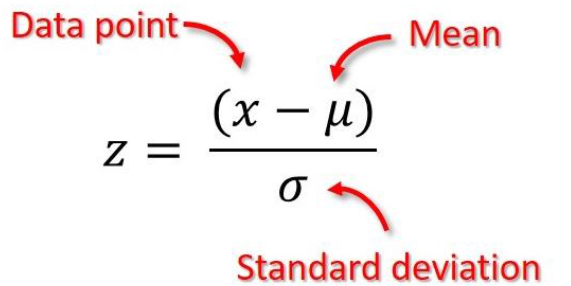
Như vậy những điểm có z score có thể coi là ngoại lại thì nó nằm ngoài đoạn [-3, 3]. Biến đổi toán học một chút, việc này tương đương với việc các điểm nằm ngoài đoạn [μ−3σ,μ+3σ] được coi là các điểm ngoại lệ.

class ZscoreOutlierClipper(BaseEstimator, TransformerMixin):
    def __init__(self, z_threshold: float = 3):
        self.z_threshold = z_threshold
        self.lower = None
        self.upper = None

    def fit(self, X: pd.Series):
        mean = X.mean()
        std = X.std()
        self.lower = mean - self.z_threshold * std
        self.upper = mean + self.z_threshold * std
        return self

    def transform(self, X):
        return X.clip(self.lower, self.upper)

Áp dụng thử với ví dụ bên trên

clipped_total_rooms2 = ZscoreOutlierClipper().fit_transform(df_housing["total_rooms"])
clipped_total_rooms2.hist(bins=50);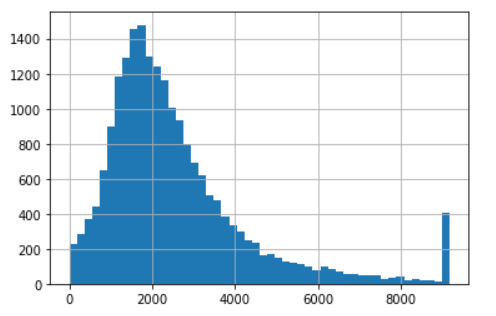

Nhận xét:

So với box plot, z score trong trường hợp này trả về khoảng giá trị rộng hơn, các giá trị lớn hơn 9000 mới được coi là ngoại lệ trong khi con số chặn trên của boxplot chỉ khoảng 6000.
Khi z score xử lý ngoại lệ có thể làm dịch chuyển kỳ vọng và độ lệch chuẩn do vậy giá trị chặn trên và chặn dưới cũng sẽ có thay đổi. Nghĩa là lần xác định tiếp theo sẽ khác so với lần hiện tại.
Còn với IQR dù giá trị ngoại lai có như thế nào cũng sẽ không làm ảnh hưởng tới chặn trên và dưới, vì nó chỉ cần thay giá trị ngoại lai vào giá trị chặn trên hoặc dưới.

Cách xác định và xử lý các điểm ngoại lai là categorical.

Khác với dữ liệu là số, dữ liệu ngoại lệ trong các trường categorical khó xác định hơn. Một phần là khó sẽ biểu đồ histogram và muốn xác định dữ liệu ngoại lệ cần có kiến thức chuyên môn cao.

Với giá trị ngoại lệ có thể xảy ra ở một trong các trường hợp sau:
Do sai khác về cách nhập liệu. Ví dụ như tên các thành phố, do vậy ta cần đưa chúng về một dạng chuẩn hóa để dễ loại bỏ các điểm ngoại lệ.
Hoặc có thể là nhập sai lỗi chính tả, để xử lý chúng ta có thể vẽ histogram thể hiện tần suất của từng giá trị trong toàn bộ dữ liệu. Thông thường những lỗi chính tả thì nó sẽ ở mức thấp.
Đối với một số dữ liệu có liên quan tới dữ liệu nhãn mà chúng có nhiều dữ liệu khác nhau khó one-hot hay enlable thì ta có thể nhóm chúng thày những mục mới có điểm chung. Ví dụ: Tên số nhà, thì ta có thể xác định nhà đó ở trong ngách, trong ngõ hay ngoài đường lớn từ đó xác định giá nhà.

Tổng kết:

Bài viết này đã đề cập tới việc nhận diện outlier trên dữ liệu là số hoặc dữ liệu là một danh mục và xử lý chúng bằng hai phương pháp: IQR hay Z score.