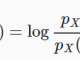

GDA và Naive Bayes trong machine learing
- 15-09-2021
- chuong xuan
- 0 Comments
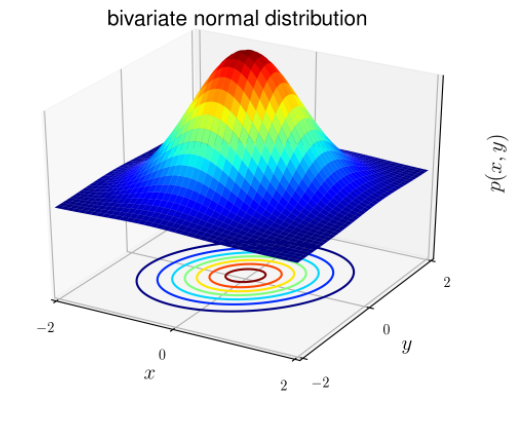
Phân phối chuẩn hay còn được gọi là phân phối Gauss (hình chuông). Phân phối có dạng tổng quát giống nhau, chỉ khác tham số vị trí (giá trị trung bình μ) và tỉ lệ (phương sai σ2).

Phân phối Gaussian có dạng:

Trong đó:
- Mean vector (kỳ vọng): μ ∈ Rd
- Covariance matrix (ma trận hiệp phương sai): Σ ∈ Rdxd
Đối với các bài toán phân lớp (classification), x là biết ngẫu nhiên liên tục (khi x là liên tục thì giá trị có thể có của nó lấp đầy một khoảng trên trục số X ∈ (xmin; xmax). Chúng ta có thể sử dụng mô hình Gaussian Discriminant Analysis (GDA): dự đoán xác suất P(x|y) dựa theo phân phối chuẩn nhiều biến.
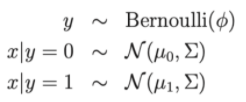
Viết dưới dạng phân phối:
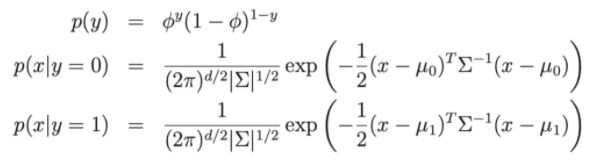
Trong đó:
- Tham số mô hình ∅, Σ , μ0, μ1 .
- μ0, μ1 là 2 vector trung bình của x|y = 0 và x|y = 1
- Hàm mất mát của mô hình: Log-linkihood
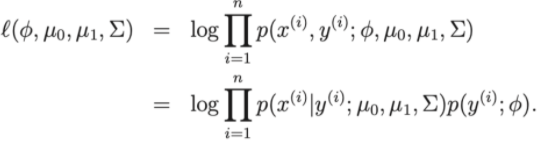
Như vậy để cực tại hàm mất mát ta có thể quy bài toán về tìm các tham số ∅, Σ , μ0, μ1 của tập dữ liệu huấn luyện.
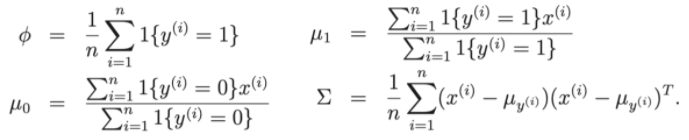
Cùng thảo luận một số vấn đề giữa GDA và Logistic regression nào.
Giả sử nếu ta coi p(y=1 | ∅, Σ , μ0, μ1 ) là một hàm của x, thì lúc này biểu thức sẽ có dạng:
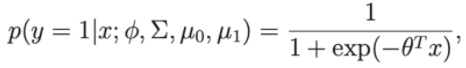
Với theta là một xấp xỉ của ∅, Σ , μ0, μ1
Như vậy ta thấy nó có dạng giống như dạng của thuật toán logistic regression.
- Vậy nếu phân bố của p(x | y) có dạng phân bố Gauss thì GDA tốt
- Nếu phân bố của p(x | y) không theo phân phối Gauss thì GDA có thể kém hiệu quả hơn.
Mục lục
Thuật toán phân lớp Naive Bayes
Giả sử như thuật toán phân loại khách hàng hoặc phân loại email là spam hay non-spam. Nếu biểu diễn email thành vector đặc trưng có số chiều bằng kích thước của từ điển. Nếu trong email có từ thứ j trong từ điển thì xj = 1 ngược lại xj = 0. Và điều gì sẽ xảy ra nếu bộ từ điểm gồm 5000 từ, x ∈ {0, 1}5000 . Như vậy nếu muốn xây dựng bộ phân lớp thì cần tối thiểu 2(50000-1) tham số và đó không phải là một con số nhỏ.
Để mô hình hóa p(x | y) ta giả sử xi là độc lập. Việc giả sử này gọi là Naive Bayes (ngây thơ). Kết quả của thuật toán là Naive Bayes classificer.
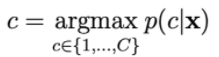
Xác suất p(c | x) được tính bằng cách:
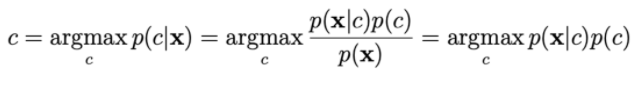
Để tính p(x|c), ta dựa vào giả sử xi độc lập với
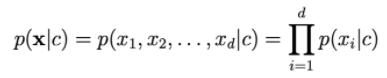
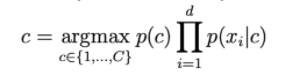
Khi d càng lớn, ta thấy xác suất vế ohari càng nhỏ. Do vậy ta cần lấy log vế phải để scale nó lên.
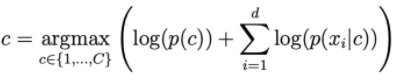
Các phân phố thường dùng trong NBC.
1. Guassian naive Bayes:
Với mỗi chiều dữ liệu i và một class c, xi tuân theo một phân phối chuẩn có kì vọng μci và phương sai σci2 .
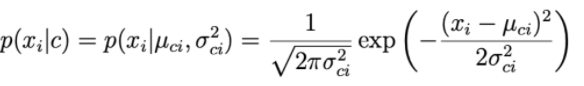
Tham số μci và phương sai σci2 được xác định dựa trên các điểm trong traning set thuộc class c.
2. Bernoulli Naive Bayes
Thành phần của vector đặc trưng là các biến rời rạc nhận giá trị 0 hoặc 1: Khi đó p(xi|c) được tính bằng:
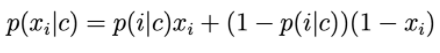
p(i|c) có thể được hiểu là xác suất từ thứ i xuất hiện trong văn bản của class c.
3. Multinomial Naive Bayes:
Thành phần của vector đặc trưng là các biến rời rạc theo phân phối Poisson.
Giả sử bài toán phân loại văn bản với x là biểu diễn Bow.
Giá trị của thành phần thứ i trong mỗi vector là số lần từ thứ i xuất hiện trong văn bản.
Khi đó, p(xi|c) tỉ lệ với tuần suất từ thứ i xuất hiện trong các văn bản của class c.
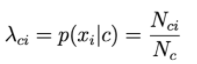
Nci là tổng số lần thứ i xuất hiện trong các văn bản của class c.
Nc là tổng số từ (kể cả lặp) xuất hiện trong class c.
4. Laplace smoothing.
Nếu có 1 từ chưa bao giờ xuất hiện trong class c thì xác suất về phải của công thức sau sẽ = 0.
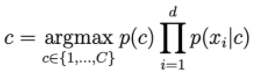
Để giải quyết việc này, một kỹ thuật được gọi là Laplace smoothing được áp dụng:
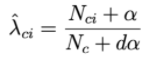
Trong đó α là một số dương, thường thì α sẽ bằng 1, mẫu cộng với dα giúp đảm bảo tổng xác suất. Như vậy, mỗi class c sẽ được mô tả bởi một bộ phận các số dương có tổng bằng 1.